Solutions of ${sin}^{- 1} (sin x) = sin x are if x \in (0, 2 π)$

A

4 real roots

B

2 positive real roots

C

2 negative real roots

D

5 real roots

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

By graph

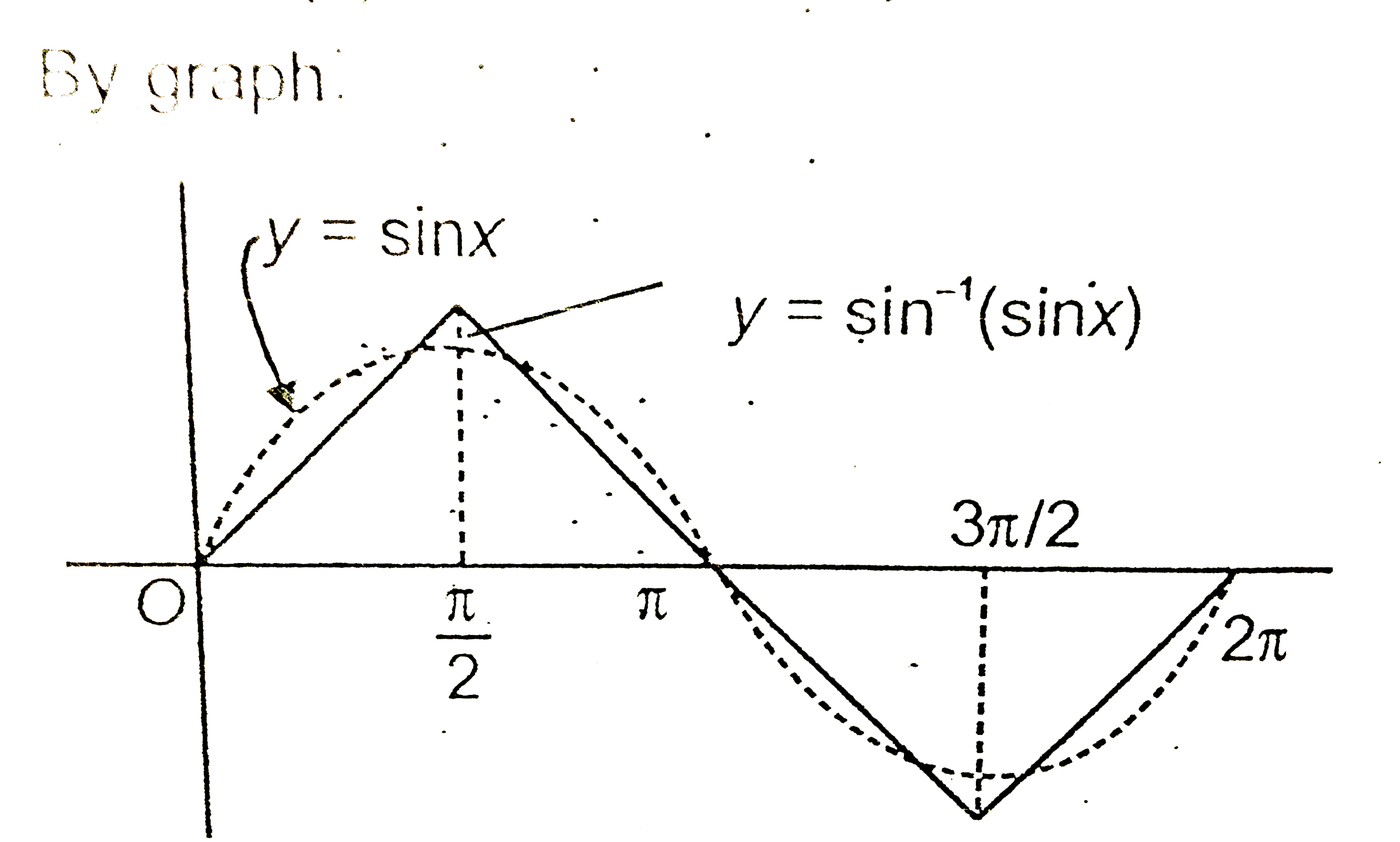
Option 4 is correct.

|

Updated on:21/07/2023

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - TRY YOURSELF
21videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))
45videos
INVERSE TRIGONOMETRIC FUNCTIONS
BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Try yourself
50videos
INTEGRALS
BOOK - AAKASH INSTITUTECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j
3videos
LIMITS AND DERIVATIVES

Similar Questions

Knowledge Check

Question 1 - Select One
Total number of solutions of ${sin}^{4} x + {cos}^{4} x = sin x \cdot cos x$ in $[0, 2 π]$ is equal to
A2
B4
C6
D8
Question 2 - Select One
General solution of ${sin}^{2} x + sin x = 2$ is
A $\frac{n π}{2} + {(- 1)}^{n} \frac{π}{4}, n \in Z$
B $\frac{n π}{2} + {(- 1)}^{n} \frac{π}{2}, n \in Z$
C $(n π) + {(- 1)}^{n} \frac{3 π}{2}, n \in Z$
D $n π + {(- 1)}^{n} \frac{π}{2}, n \in Z$
Question 3 - Select One
The value of ${sin}^{- 1} (cos (cos x) + {sin}^{- 1} (sin x)))$ where $x \in (\frac{π}{2}, π)$ is equal to
A $- π / 2$
B $π / 2$
C $- π$
D $π$

AAKASH INSTITUTE-INVERSE TRIGONOMETRIC FUNCTIONS-ASSIGNMENT (SECTION - J)(ANKASH CHALLENGERS QUESTIONS)

Home
Ask Doubt
Profile