A,B,C and D have mixed up their respective secret codes in an envelope in How many ways can they pick up their codes in such a manner that no one gets his own code ?
Video Solution
Text Solution
Let a,b,c,d respectively represent codes of A,B,C,D when codes a,b,c,d are mixed up they can be picked up in 4!=24 ways
But codes have been picked up so that A does not get a,B does not get b,C does not get c and D does not get d. Hence problem reduces to total number of derangement of a,b,c,d.
=4![1−11!+12!−13!−14!]=9
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself65videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )51videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions3videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)12videos
PRINCIPLE OF MATHEMATICAL
Similar Questions
Knowledge Check
- Question 1 - Select One
A person buys a book for 85 and sells it for 98.60. Find the profit percent.
A6B12C16Dnone of these - Question 2 - Select One
There are 4 different letters and 4 addressed envelopes. In how many ways can the letters be put in the envelopes so that atleast one letter goes to the correct address?
Aa. 15Bb. 16Cc. 18Dd. 12 - Question 3 - Select One
Match the List-I with List-II and pick up the correct matching from the codes given below:
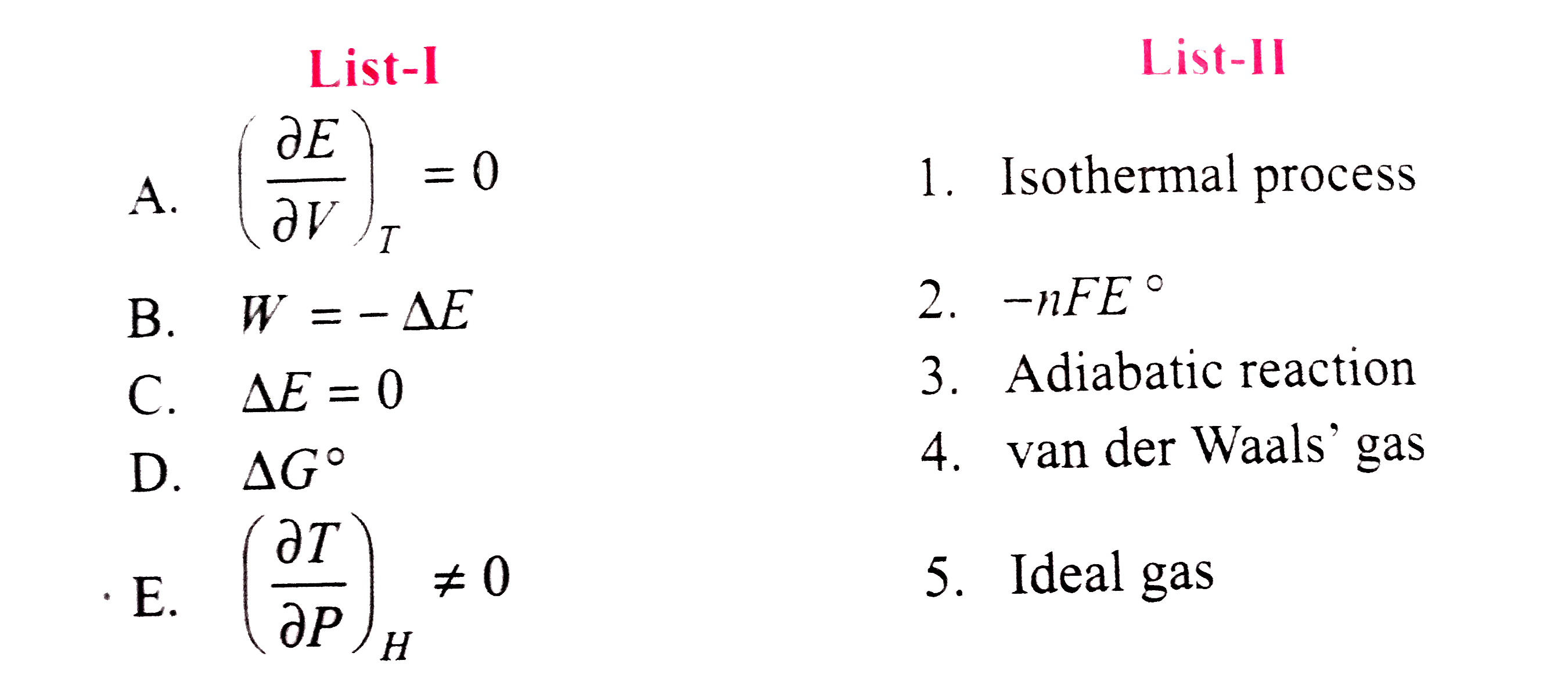 AA-2 B-1 C-4 D-5 E-3BA-2 B-5 C-1 D-4 E-3CA-3 B-1 C-2 D-5 E-4DA-5 B-3 C-1 D-2 E-4
AA-2 B-1 C-4 D-5 E-3BA-2 B-5 C-1 D-4 E-3CA-3 B-1 C-2 D-5 E-4DA-5 B-3 C-1 D-2 E-4
Match List I with List II and pick up the correct choice from the under assigned codes
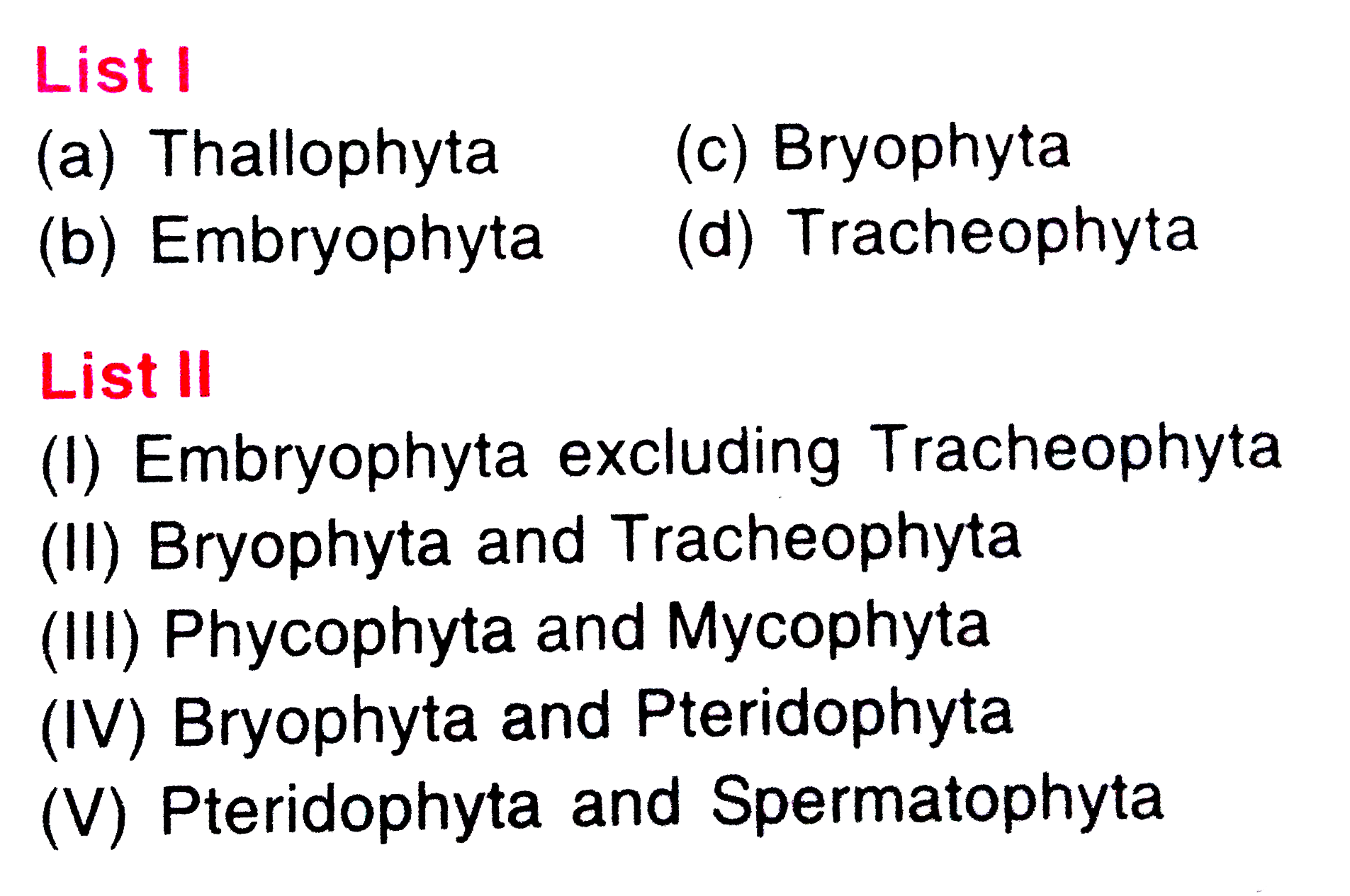 View Solution
View SolutionIn how many ways we can put 5 letters into 5 corresponding envelopes so that atleast one letter go the wrong envelope?
View SolutionSix persons A, B, C, D, E, F, are to be seated at a circular table. In how many ways antis be one if A should have either B or C on his right and B must always have either C or D on his right.
View SolutionIn how many different ways can a person get his two guests stayed in 9 rooms, when only one guest is stayed in one room?
View SolutionAssertion. One of the property of genetic code is degeneracy.
Reason. Many amino acids can be coded by more than one codon.View Solution

