A balloon is rising vertically from a level field , suppose an on-looker sees it rising at 0.14 rad/min. when θ=π4 (when the on -looker is 500 m away from the launch spot ), how fast is balloon rising ?
Given , dθdt=0.4
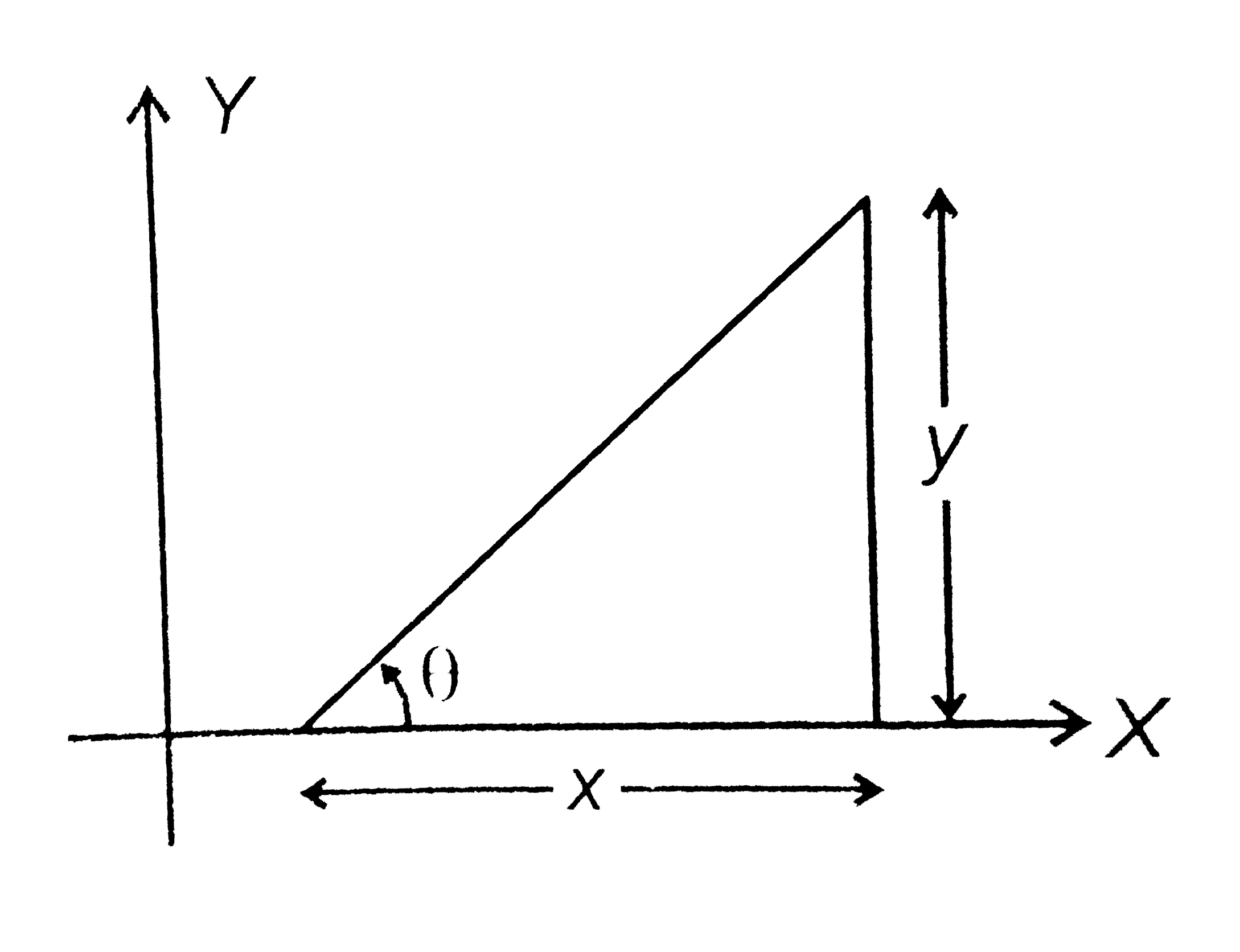
In given figure ,
tanθ=y500
Differentiate with respect to t
sec2θdθdt=1500dydt
(dydt)θ=π4=500×2×0.14=140 m/min.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - TRY YOURSELF39videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-A (Competition Level Questions)50videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions2videos
APPLICATION OF INTEGRALS
Similar Questions
A hot-air balloonist, rising vertically with a constant velocity of magnitude 20ms−1, releases a sandbag at an instant when the balloon is 25m above the ground . Afere it is released, the sandbag is in free fall. Skerch ay−t,vy−t, and y−t graphs for motion, taking origin at ground.
 .View Solution
.View SolutionA balloon and a bicycle. A balloon is rising vertically above a level, straight road at a constant rate of 1 ft/sec. Just when the balloon is 65 ft above the ground , a bicycle moving at a constant rate of 17 ft/sec passes under it . How fast is the distance between the bicycle and balloon increasing 3 sec later ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
balloon is rising vertically up with a velocity of 29 m/s. A stone is dropped from it and it reaches the ground in 10 seconds. The height of the balloon when the stone was dropped from it is (g=9.8ms2)
A100mB200mC400mD150m - Question 2 - Select One
A man in a balloon rising vertically with an acceleration of 4.9m/sec2 , releases a ball 2 seconds after the balloon is let go from the ground. The greatest height above the ground reached by the ball is
A14.7mB19.6 mC9.8mD24.5 m
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance? How far is the foot from the wall when it and the top are moving at the same rate?
View SolutionA balloon is rising vertically upwards. An an instant, an observation on the ground, whose distance from the balloon is 100 meters, sees the balloon at an angle of elevation of 30∘. If the balloon rises further vertically to a point where the angle of elevation as seen by the observer is 45∘, then its height (in meters) from the ground is
(Take √3=1.73)View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multi-storey building. The height of the point from where the boll is thrown is 25.0m from the ground (a) How high will the ball rise? and (b) How long will it take to reach the ground?
View SolutionA ball is thrown vertically upwards with a velcotiy of 20ms−1 from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25-0m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. g=10ms−2.
View SolutionA hot air balloon rising straight up from a level field is tracked by a range finder 500 ft from the lift-off point. At the moment the range finder's elevation angle is π4. The angle is increasing at the rate of 0.14 rad/min. How fast is the balloon rising at the moment ?
 View Solution
View SolutionA hot air balloon rising straight up from a level field is tracked by a range finder 500 ft from the lift-off point. At the moment the range finder's elevation angle is π4, the angle is increasing at the rate of 0.14 rad/min. How fast is the balloon rising at that moment.
View Solution

