Prove that G→A+G→B+G→C=→0, if G is the centroid of Δ ABC.
Let →a,→b and →c be the position vectors of the vertices A,B and C of a triangle ABC, respectively. Then the position vector of the centroid G is →a+→b+→c3
Now G→A+G→B+G→C
=→a−(→a+→b+→c3)+→b(→a+→b+→c3)+→c(→a+→b+→c3)
=(→a+→b+→c)−(→a+→b+→c)=→0
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - ILLUSTRATION1videos
VECTOR ALGEBRA
- BOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF20videos
VECTOR ALGEBRA
- BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)15videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If A, B, C are vertices of a triangle whose position vectors are →a,→band→c respectively and G is the centroid of ΔABC, then −−→GA+−−→GB+−−→GC, is
A→0B→a+→b+→cC→a+→b+→c3D→a−→b−→c3 - Question 2 - Select One
Find the ratio of the areas of an equilateral triangle ABC and square EFGC, if G is the centroid of the triangle ABC.
 A27:16B1:4C4:3√3D3√3:4
A27:16B1:4C4:3√3D3√3:4 - Question 3 - Select One
If G is the centroid of ΔABCandG' is the centroid of ΔA'B'C' then −−→AA'+−−→BB'+−−→CC'=
A2−−→GG'B3−−→GG'C−−→GG'D4−−→GG'
If G is the centroid of △ABC,prove that −−→GA+−−→GB+−−→GC=0. Further if G1 bet eh centroid of another △PQR, show that −−→AP+−−→BQ+−−→CR=3−−−→GG1
View SolutionLet a=BC,b=CA,C=AB be the sides of the triangle ABC. If G is the centroid of ΔABC such that GB and ¯¯¯¯¯¯GCand¯¯¯¯¯¯GC are inclined at an obtuse angle, then
View Solution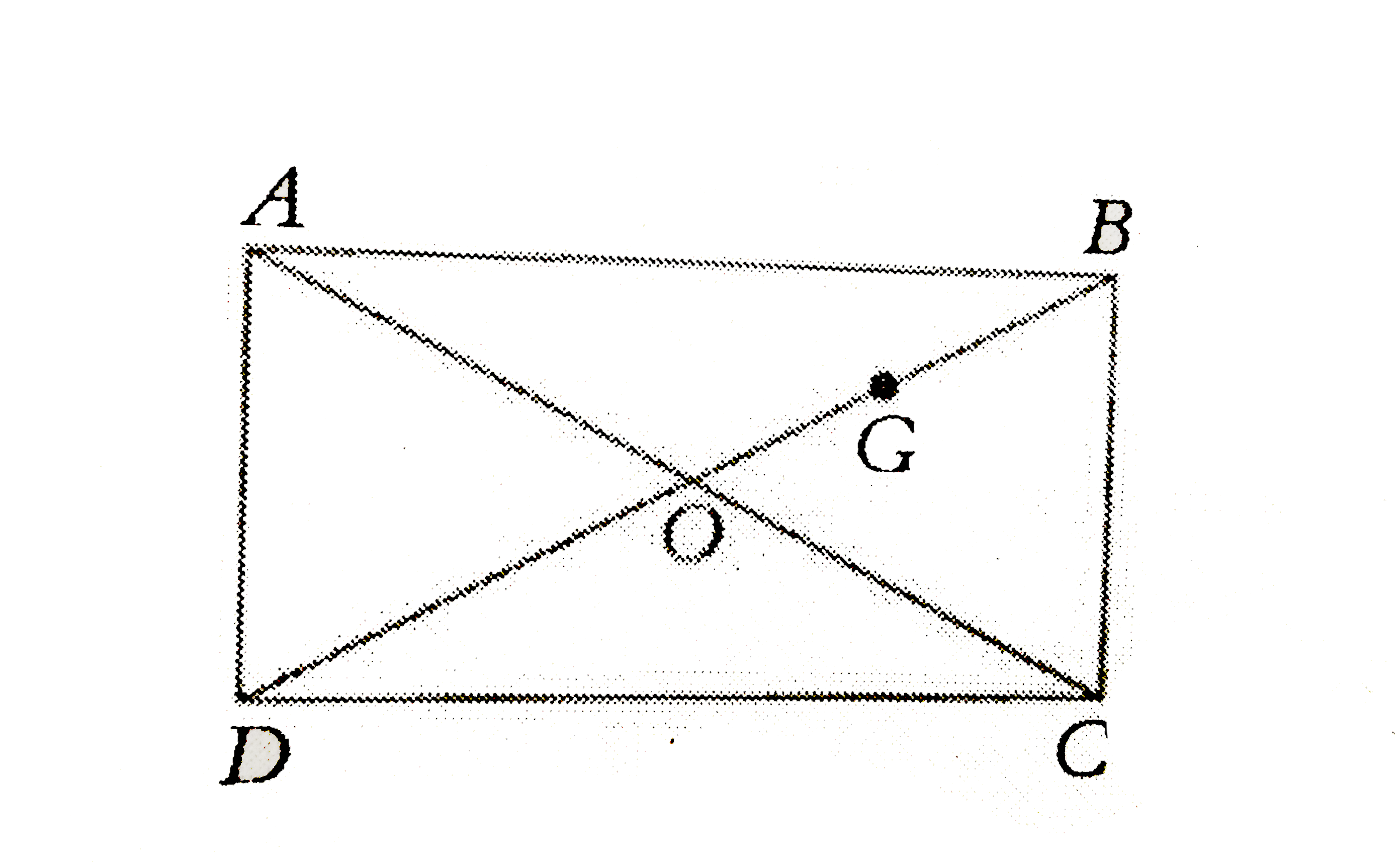
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC . If BG=4 cm, then find the length of AC.View SolutionIf G is the centroid of ΔABCandG' is the centroid of the ΔA'B'C',andAA'+BB'+CC'=KGG, then K is equal to
View SolutionABC is an equilateral triangle with side 12cm and AD is the median. Find the length of GD if G is the centroid of △ABC.
ABC एक समबाहु त्रिभुज है जिसके भुजा 12cm और AD मध्यिका है। GD की लंबाई ज्ञात करें यदि G,△ABC का केन्द्रक है।View Solution

