The playground of our school is in the shape of a quadrilateral ABCD. A flagpost standing vertically in the ground subtends angles of 45∘and30∘ at two points P and Q, which lie on the sides AB and AD respectively such that AP = 50 m and AQ = 30 m. If P and Q are the nearest points on the sides AB and AD to the flagpost, then the height of the flagpost is :
Step by step video & image solution for The playground of our school is in the shape of a quadrilateral ABCD. A flagpost standing vertically in the ground subtends angles of 45^@ and 30^@ at two points P and Q, which lie on the sides AB and AD respectively such that AP = 50 m and AQ = 30 m. If P and Q are the nearest points on the sides AB and AD to the flagpost, then the height of the flagpost is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32ACIn the adjoining figure, P and Q are two points on equal sides AB and AC of a isosceles triangle ABC such that AP = AQ, then
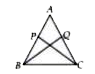 ABQ = CPB∠ABQ=∠ACPC∠BAQ=∠CPADboth (a) and (b)
ABQ = CPB∠ABQ=∠ACPC∠BAQ=∠CPADboth (a) and (b)A circle touches the sides of a quadrilateral ABCD at P, Q, R and S respectively. Find the angles subtended at the centre by a pair of opposite sides.
A180∘B270∘C225∘DNone of these
P and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionABCD is a square. P, Q, R, S are points on the sides AB. BC, CD, DA respectively such that AP = BQ = CR = DS. What is ∠SPQ equal to ?
View SolutionIn the adjoining figure, P and Q are two points on equal sides AB and AC of an isosceles triangle ABC such that AP = AQ. Prove that BQ = CP.
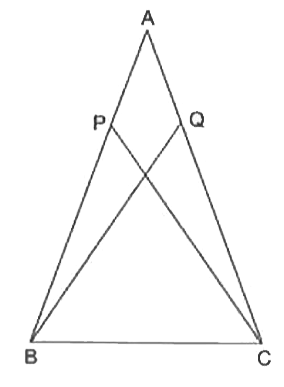
View SolutionA vertiacal pole is 60 m high, The angle of depression of two points P and Q on the ground are 30∘and45∘ respectively. If the points P and Q lie on either side of the pole, then find the distance PQ.
View Solution
