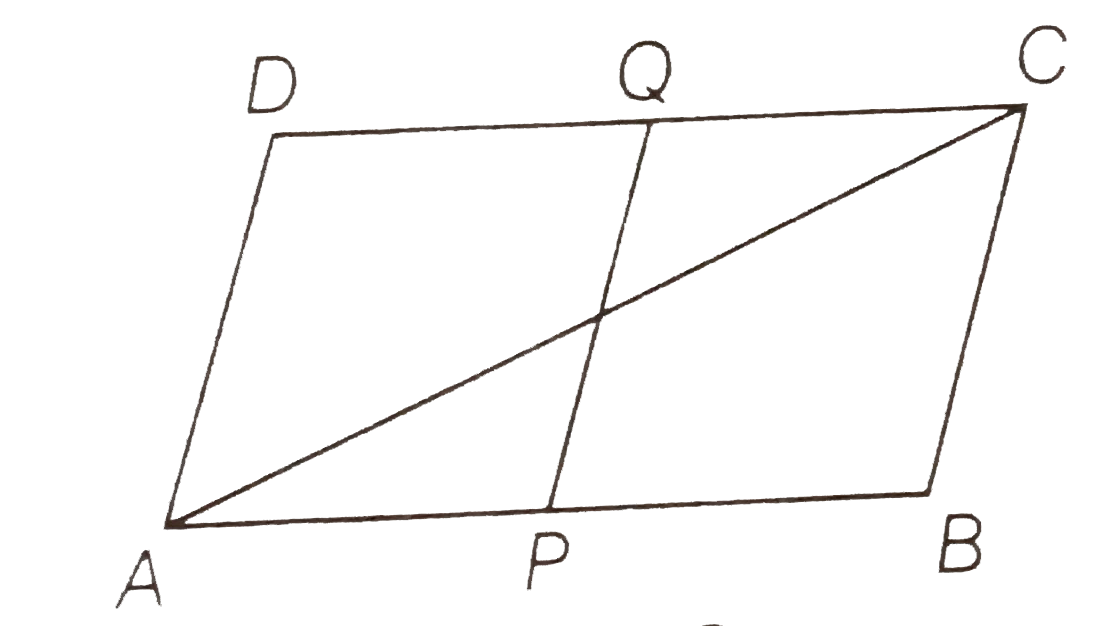
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to

A

AC

B

$\frac{1}{2} A C$

C

$\frac{2}{3} A C$

D

$\frac{3}{2} A C$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

To solve the problem, we need to find the sum of the vectors $\to A P + \to A Q$ where $P$ and $Q$ are the midpoints of sides $B C$ and $C D$ of the parallelogram $A B C D$ .
1. Identify Points and Vectors:
Let the position vectors of points $A, B, C, D$ be represented as $\to A, \to B, \to C, \to D$ respectively. Since $A B C D$ is a parallelogram, we have:
$\to C = \to A + \to B - \to D$
2. Find Midpoints $P$ and $Q$ :
The midpoint $P$ of side $B C$ can be expressed as:
$\to P = \frac{\to B + \to C}{2}$
The midpoint $Q$ of side $C D$ can be expressed as:
$\to Q = \frac{\to C + \to D}{2}$
3. Express $\to A P$ and $\to A Q$ :
The vector $\to A P$ is given by:
$\to A P = \to P - \to A = (\frac{\to B + \to C}{2}) - \to A$
The vector $\to A Q$ is given by:
$\to A Q = \to Q - \to A = (\frac{\to C + \to D}{2}) - \to A$
4. Substituting $\to C$ :
Substitute $\to C = \to A + \to B - \to D$ into the equations for $\to A P$ and $\to A Q$ :
$\to A P = \frac{\to B + (\to A + \to B - \to D)}{2} - \to A = \frac{2 \to B + \to A - \to D}{2} - \to A = \frac{2 \to B - \to A - \to D}{2}$
$\to A Q = \frac{(\to A + \to B - \to D) + \to D}{2} - \to A = \frac{\to A + \to B}{2} - \to A = \frac{\to B - \to A}{2}$
5. Adding $\to A P$ and $\to A Q$ :
Now, we can add $\to A P$ and $\to A Q$ :
$\to A P + \to A Q = (\frac{2 \to B - \to A - \to D}{2}) + (\frac{\to B - \to A}{2})$
Combine the terms:
$= \frac{(2 \to B - \to A - \to D) + (\to B - \to A)}{2} = \frac{3 \to B - 2 \to A - \to D}{2}$
6. Expressing in terms of $\to A C$ :
Since $\to A C = \to C - \to A$ :
$\to A C = \to A + \to B - \to D - \to A = \to B - \to D$
Therefore, we can express $\to A P + \to A Q$ in terms of $\to A C$ :
$\to A P + \to A Q = \frac{3}{2} \to A C$
Conclusion:
Thus, we find that:
$\to A P + \to A Q = \frac{3}{2} \to A C$

|

Updated on:7/8/2024

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS ENGLISH-VECTOR ALGEBRA-Exercise (Single Option Correct Type Questions)

Home
Ask Doubt
Profile