Statement -1 : The graph between - Kinetic energy and vertical displacement is a stright line for a projectile.
Statement -2 : The graph between kinetic energy and horizontal displacement is a straight is straight line for a projectile.
Statement -3 : the graph between kinetic energy and time is a parabola for a projectile.
F F F
T T F
T F T
F F T
The correct Answer is:3
To analyze the statements regarding the graphs of kinetic energy (KE) in projectile motion, we will evaluate each statement step by step.
Step 1: Understanding Kinetic Energy in Projectile Motion
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the projectile and v is its velocity. In projectile motion, the velocity has both horizontal and vertical components.
Step 2: Analyzing Statement 1
Statement 1: The graph between kinetic energy and vertical displacement is a straight line for a projectile.
- The vertical displacement h can be expressed as:
h=usinθ⋅t−12gt2
- The vertical component of velocity vy is given by:
vy=usinθ−gt
- The total velocity v can be expressed as:
v2=(ucosθ)2+(usinθ−gt)2
- Substituting v into the kinetic energy formula, we can see that as vertical displacement changes, the kinetic energy will change linearly with respect to vertical displacement because the vertical velocity changes linearly with time.
Conclusion for Statement 1: True.
Step 3: Analyzing Statement 2
Statement 2: The graph between kinetic energy and horizontal displacement is a straight line for a projectile.
- The horizontal displacement x is given by:
x=ucosθ⋅t
- The horizontal component of velocity vx remains constant:
vx=ucosθ
- As time progresses, the vertical component of velocity changes due to gravity, which means that the kinetic energy will not change linearly with horizontal displacement. Instead, it will vary as a function of both horizontal and vertical components, leading to a non-linear relationship.
Conclusion for Statement 2: False.
Step 4: Analyzing Statement 3
Statement 3: The graph between kinetic energy and time is a parabola for a projectile.
- As time progresses, the vertical component of velocity changes, which affects the kinetic energy. The relationship between kinetic energy and time can be derived from:
KE=12m(u2cos2θ+(usinθ−gt)2)
- This expression is quadratic in terms of time t because of the −gt term, leading to a parabolic relationship.
Conclusion for Statement 3: True.
Final Summary of Statements
- Statement 1: True
- Statement 2: False
- Statement 3: True
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the projectile and v is its velocity. In projectile motion, the velocity has both horizontal and vertical components.
Statement 1: The graph between kinetic energy and vertical displacement is a straight line for a projectile.
h=usinθ⋅t−12gt2
- The vertical component of velocity vy is given by:
vy=usinθ−gt
- The total velocity v can be expressed as:
v2=(ucosθ)2+(usinθ−gt)2
- Substituting v into the kinetic energy formula, we can see that as vertical displacement changes, the kinetic energy will change linearly with respect to vertical displacement because the vertical velocity changes linearly with time.
Statement 2: The graph between kinetic energy and horizontal displacement is a straight line for a projectile.
x=ucosθ⋅t
- The horizontal component of velocity vx remains constant:
vx=ucosθ
- As time progresses, the vertical component of velocity changes due to gravity, which means that the kinetic energy will not change linearly with horizontal displacement. Instead, it will vary as a function of both horizontal and vertical components, leading to a non-linear relationship.
Statement 3: The graph between kinetic energy and time is a parabola for a projectile.
KE=12m(u2cos2θ+(usinθ−gt)2)
- This expression is quadratic in terms of time t because of the −gt term, leading to a parabolic relationship.
- Statement 1: True
- Statement 2: False
- Statement 3: True
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)4videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -G (Integer)3videos
MOTION IN A PLANE
- BOOK - AAKASH INSTITUTECHAPTER - MOCK_TEST_17EXERCISE - Example15videos
MOCK_TEST_17
- BOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)15videos
MOTION IN A STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
In S.H.M., the graph between kinetic energy K and time 't' is
A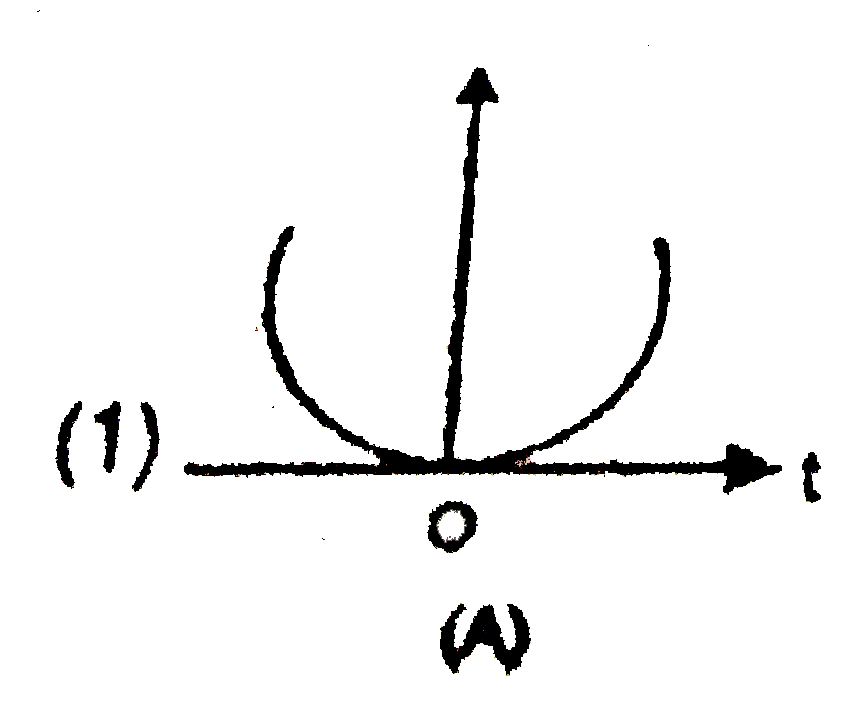 B
B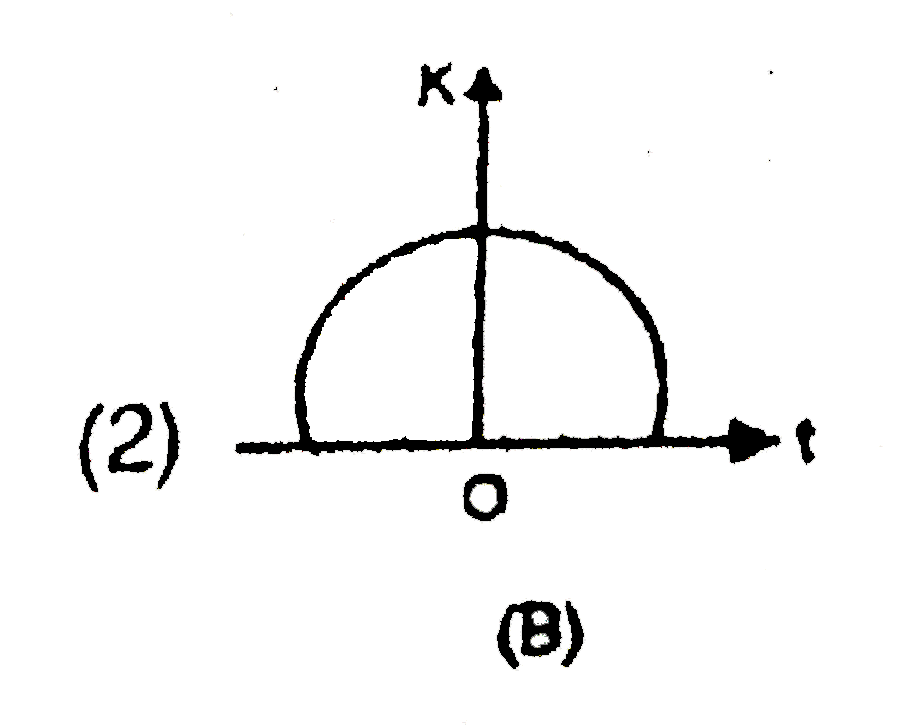 C
C D
D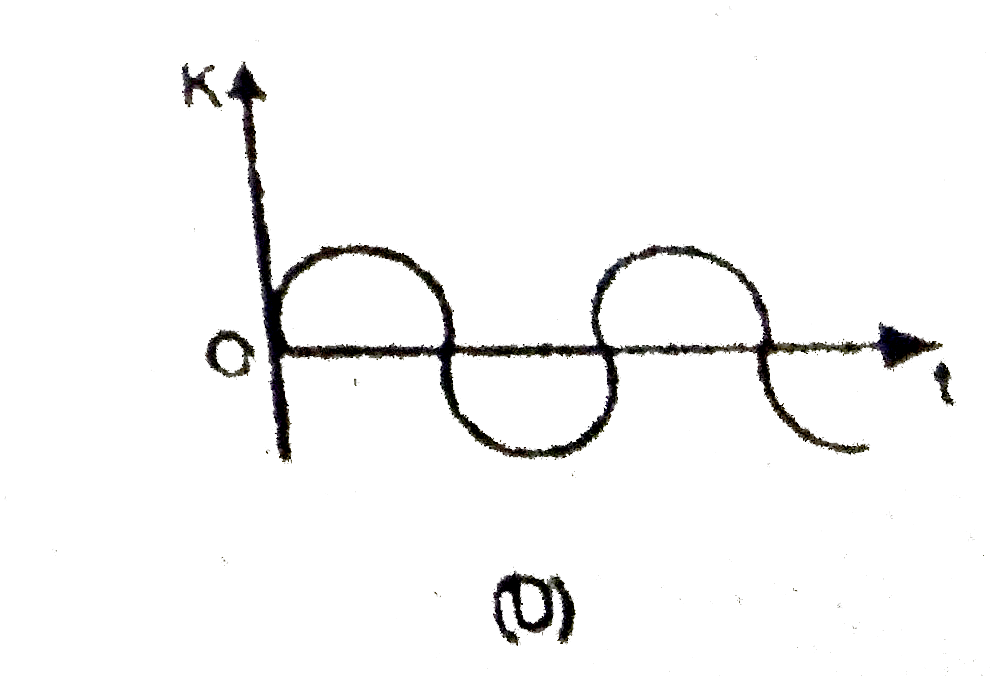
- Question 2 - Select One
Which of the graph between kinetic energy and time is correct ?
AABBCEDF - Question 3 - Select One
The graph between kinetic energy and displacement of a particle performing S.H.M. is
AparabolaBstraight lineCellipseDcircle
The graph between total energy and displacement of a particle performing S.H.M. is
View SolutionThe graph between potential energy U and displacement X in the state of stable equilibrium will be–
View SolutionA ball is thrown up with a certain velocity at an angle θ to the horizontal. The graph between kinetic energy and horizontal displacement is given by:
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionWhat is the shape of the graph between the speed and kinetic energy of a body
View Solution

