Question

Show how you would connect three resistors, each of $6\Omega$, so that the combination has a resistance of (a) 9 $\Omega$, (b) 4 $\Omega$.

Explanation

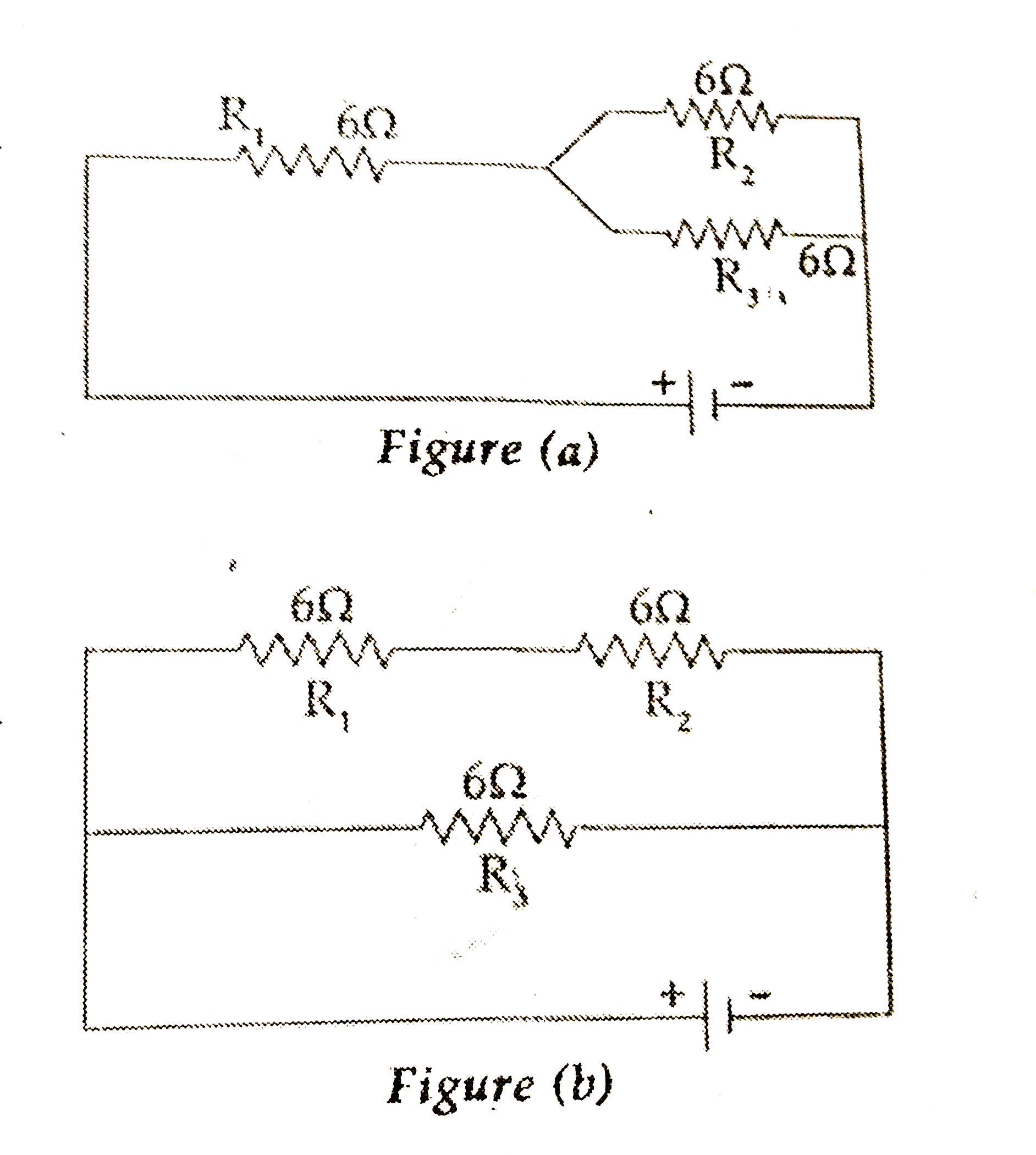
Given `R_(1)=R_(2)=R_(3)=6Omega`
(a) When `R_(1)` is connected in series with the parallel combination of `R_(2) and R_(3)` [Fig(a)].
The equivalent resistance is :
`R=R_(1)+(R_(2)R_(3))/(R_(2)+R_(3))`
`=6+(6xx6)/(6+6)=6+3=9 Omega`
(b) When a series combination of `R_(1) and R_(2)` is connected in parallel with `R_(3)` [Fig (b)].
The equivalent resistance is:
`R=(12xx6)/(12+6)=(72)/(18)=4 Omega`