How will you join three resistances, each of 2Ω so that the effective resistance is 3Ω ?
To solve the problem of how to join three resistances, each of 2Ω, so that the effective resistance is 3Ω, we can follow these steps:
1. Understanding the Configuration:
We have three resistors, each of 2Ω. We need to find a way to connect them such that the total or effective resistance equals 3Ω.
2. Trying Series Connection:
First, let's consider connecting all three resistors in series.
- The formula for total resistance in series is:
\(
R_{\text{total}} = R_1 + R_2 + R_3
\)
- Substituting the values:
\(
R_{\text{total}} = 2 Ω + 2 Ω + 2 Ω = 6 Ω
\)
- This is not equal to 3Ω, so a series connection does not work.
3. Trying Parallel Connection:
Next, let's consider connecting all three resistors in parallel.
- The formula for total resistance in parallel is:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
- Substituting the values:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{2 Ω} + \frac{1}{2 Ω} + \frac{1}{2 Ω} = \frac{3}{2 Ω}
\)
- Therefore,
\(
R_{\text{total}} = \frac{2}{3} Ω
\)
- This is also not equal to 3Ω, so a parallel connection does not work either.
4. Combining Series and Parallel:
Now, let's try a combination of series and parallel connections. We can connect two resistors in parallel and the third one in series with the combination.
- First, connect two resistors in parallel:
\(
\frac{1}{R_{\text{parallel}}} = \frac{1}{2 Ω} + \frac{1}{2 Ω} = \frac{2}{2 Ω} = 1 Ω
\)
- So, the equivalent resistance of the two resistors in parallel is 1Ω.
5. Adding the Third Resistor in Series:
Now, we add the third resistor (which is 2Ω) in series with the equivalent resistance from the parallel connection:
\(
R_{\text{total}} = R_{\text{parallel}} + R_3 = 1 Ω + 2 Ω = 3 Ω
\)
6. Conclusion:
Therefore, to achieve an effective resistance of 3Ω, we connect two resistors in parallel and one resistor in series.
Final Configuration:
- Connect two 2Ω resistors in parallel and then connect the third 2Ω resistor in series with the parallel combination.
We have three resistors, each of 2Ω. We need to find a way to connect them such that the total or effective resistance equals 3Ω.
First, let's consider connecting all three resistors in series.
- The formula for total resistance in series is:
\(
R_{\text{total}} = R_1 + R_2 + R_3
\)
- Substituting the values:
\(
R_{\text{total}} = 2 Ω + 2 Ω + 2 Ω = 6 Ω
\)
- This is not equal to 3Ω, so a series connection does not work.
Next, let's consider connecting all three resistors in parallel.
- The formula for total resistance in parallel is:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
- Substituting the values:
\(
\frac{1}{R_{\text{total}}} = \frac{1}{2 Ω} + \frac{1}{2 Ω} + \frac{1}{2 Ω} = \frac{3}{2 Ω}
\)
- Therefore,
\(
R_{\text{total}} = \frac{2}{3} Ω
\)
- This is also not equal to 3Ω, so a parallel connection does not work either.
Now, let's try a combination of series and parallel connections. We can connect two resistors in parallel and the third one in series with the combination.
- First, connect two resistors in parallel:
\(
\frac{1}{R_{\text{parallel}}} = \frac{1}{2 Ω} + \frac{1}{2 Ω} = \frac{2}{2 Ω} = 1 Ω
\)
- So, the equivalent resistance of the two resistors in parallel is 1Ω.
Now, we add the third resistor (which is 2Ω) in series with the equivalent resistance from the parallel connection:
\(
R_{\text{total}} = R_{\text{parallel}} + R_3 = 1 Ω + 2 Ω = 3 Ω
\)
Therefore, to achieve an effective resistance of 3Ω, we connect two resistors in parallel and one resistor in series.
- Connect two 2Ω resistors in parallel and then connect the third 2Ω resistor in series with the parallel combination.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Additional)Short Answer36videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Additional)Long Answer4videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Exemplar)Long Answer6videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test21videos
MAGNETIC EFFECTS OF ELECTRIC CURRENT
Similar Questions
Show how would you join three resistors, each of resistance 9Ω so that the equivalent resistance of the combination is (i) 13.5Ω , (ii) 6Ω ?
View SolutionShow how would you join three resistors, each of resistance 9Ω so that the equivalent resistance of the combination is (i) 13.5Ω(ii)6Ω?
View Solution
Knowledge Check
- Question 1 - Select One
If Four resistors each of 1Ω are connected in parallel the effective resistances will be
A0.5ΩB0.25ΩC4ΩD2Ω
Show how you would connect three resistors, each of 6Ω, so that the combination has a resistance of (a) 9 Ω, (b) 4 Ω.
View SolutionShow how you would connect three resistors, each of resistance 6Ω so that the combination has a resistance of (i) 9Ω(ii)4Ω
View SolutionShow with the help of diagrams, how you would connet three resistors each of resistance 6Ω, so that the combination has resistance of (i) 9Ω (ii) 4Ω.
View SolutionShow how you would connect three resistors, each of resistance 6Ω, so that the combination has a resistance of (1) 9Ω (ii) 4Ω.
View SolutionShow how you would connect thre resistors, each of resistance 6Ω, so that the combination has a resistance of
(i) 9Ω
(ii) 2Ω.View SolutionThree resistors, each of 2Ω, are connected together so that their total resistance is 3Ω. Draw a diagram to show this arrangement and check it by calculation.
View SolutionIn the net work each resistance is 2Ω. Find th effective resistance between AandB
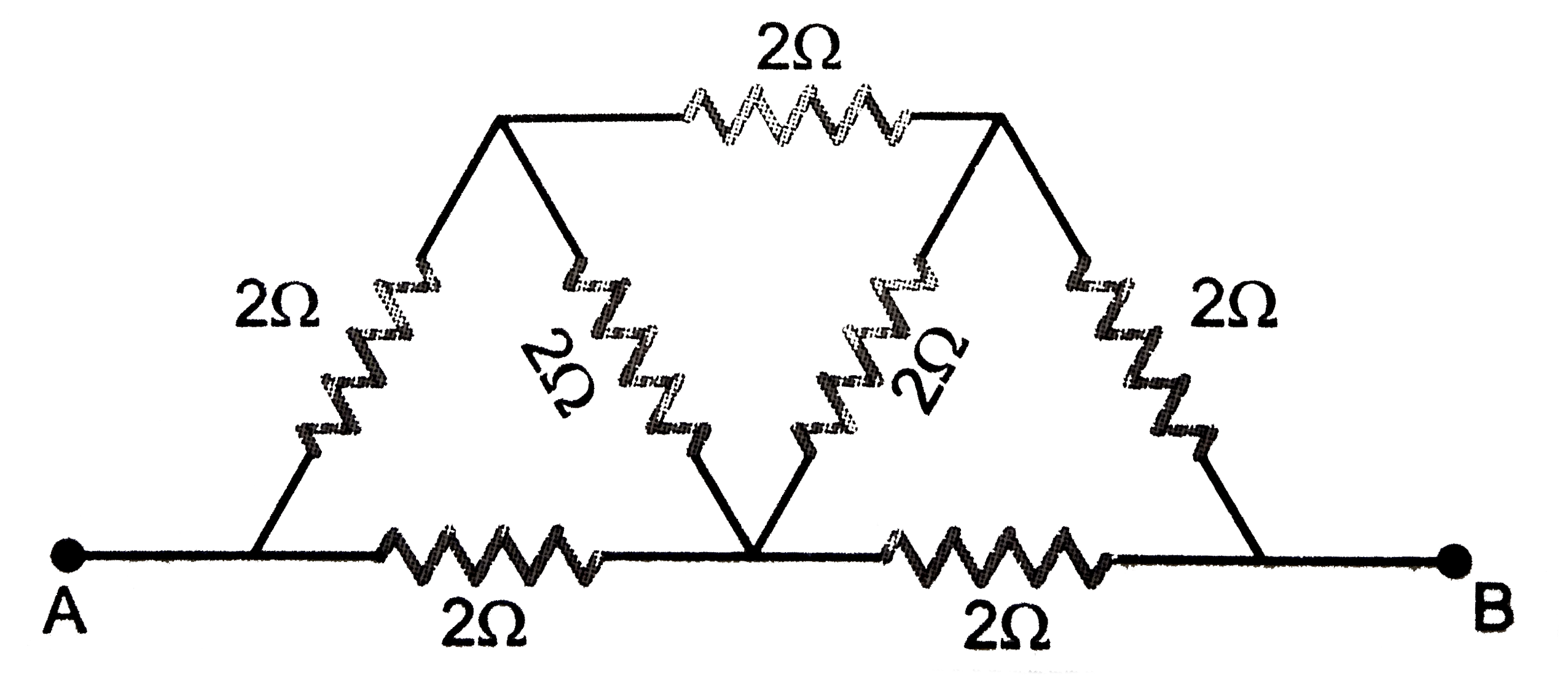 View Solution
View Solution

