बहुपद से सभी शून्यक प्राप्त कीजिए , जबकि इसके दो शून्यक और दिए गए है ।
चूँकि दिए गए बहुपद के दो शून्यक और हो तब दिए गए बहुपद का एक गुणनखण्ड होगा । अब विभाजन एल्गोरिथ्म के प्रयोग से ,

अंत :
अंत : दिए गए बहुपद के शून्यको के लिए बहुपद का मान शून्य होगा , अर्थात
और
अंत : बहुपद के सभी शून्यक और है
Topper's Solved these Questions
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नवाली 2(A)
1 Videos
- बहुपद BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(B)
15 Videos
- प्रोजेक्ट BOOK - MANOHAR RAYCHAPTER - प्रोजेक्ट EXERCISE - परीक्षा प्रश्न - पत्र, 2019
30 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(E)
25 Videos
Similar Questions
किसी बहुपद f (x ) ले लिए y =f (x ) के ग्राफ दिए है । प्रत्येक ग्राफ में f (x ) के शून्यको की संख्या कीजिए :

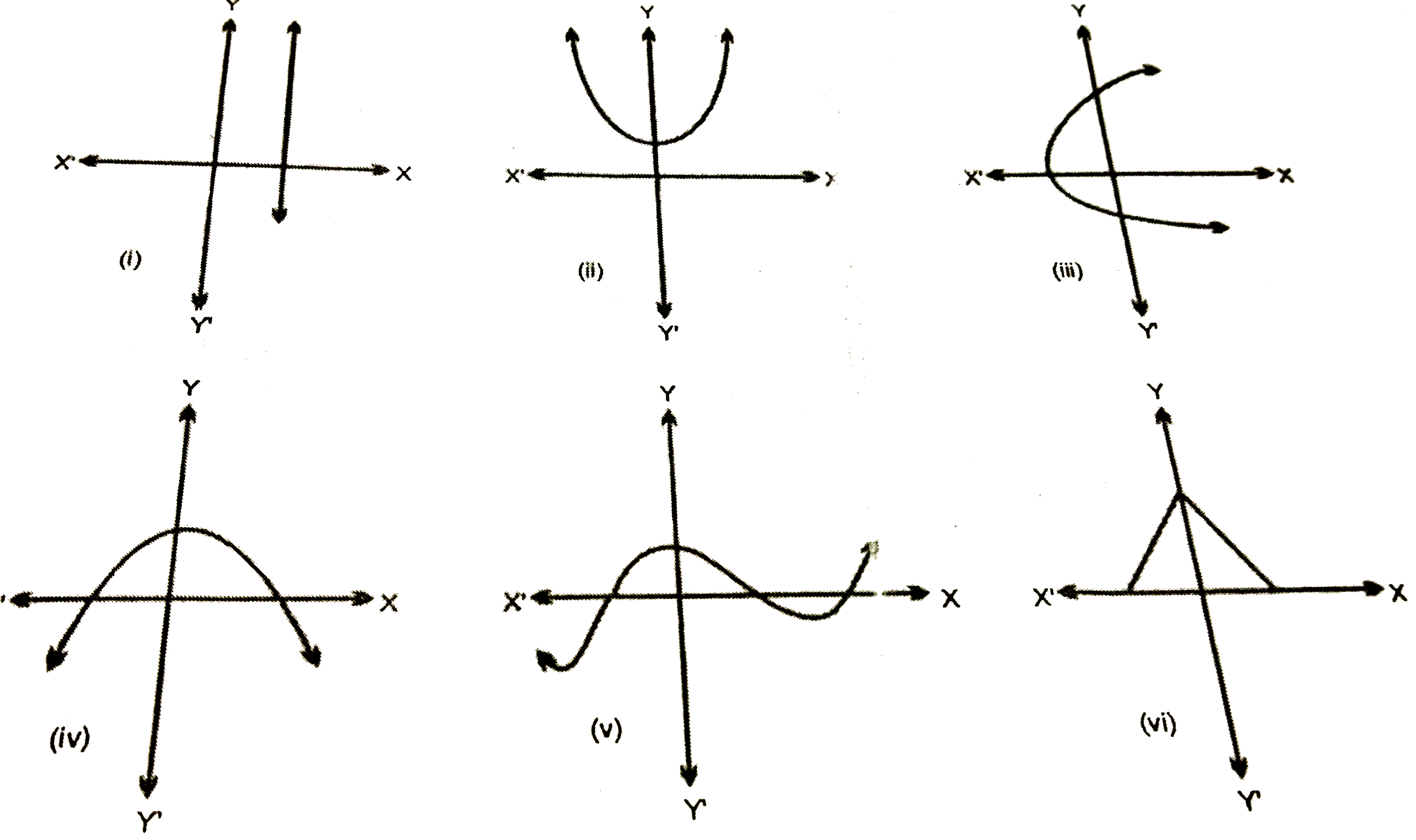
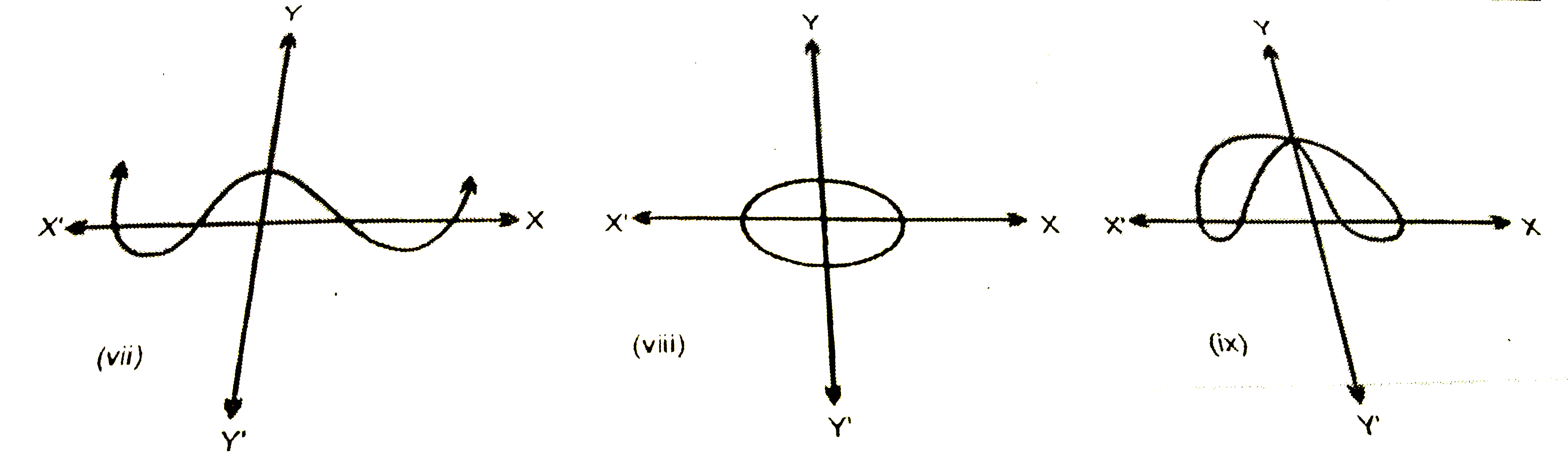
View Solutionनिम्न बहुपदो के शून्यको तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए :
(i)x2−2x−8
(ii) 4s2−4s+1
(iii)6x2−3−7x
View Solution(क) निम्नलिखित में से कौन- सा ग्राफ द्विघात समीकरण का नहीं है ?
View Solutionनिन्मलिखित में से परिमेय संख्याएँ छाँटकर लिखिए: √3,π3,2273√4,√414 और 2.33
View Solution(3sqrt(2)-2sqrt(3))/(3sqrt(2)+2sqrt(3))+(sqrt(12))/(sqrt(3)-sqrt(2))
View Solutionobtain all other zeros of the polynomial x4−3√2x3+3x2+3√2x−4. If two of its zeros are √2&2√2
View Solutionobtain all other zeroes of the polynomial x4−3√2x3+3x2+3√2x−4 , if two zeroes are √2 and 2√2
View Solutionlim_(x rarr a)(sqrt(3a+x)-2sqrt(x))/((sqrt(a+2x)-sqrt(3x)))=(3sqrt(3))/(2)
View SolutionIf x is a positive real number and x2=2, then x3= √2 (b) 2√2 (c) 3√2 (d) 4
View SolutionIf sqrt(2)=1.414 and sqrt(3)=1.732 ,find the value of (4)/(3sqrt(3)-2sqrt(2) )+(3)/(3sqrt(3)+2sqrt(2))
View Solutionनिम्न को सरल कीजिए - 3√2−2√33√2+2√3+√12√3−√2
View Solutionयदि बहुपद x4+x3−11x2−9x+18 के दो शून्यक 1 और -2 है तो इसके अन्य दो शून्यक ज्ञात कीजिए ।
View SolutionThe lines represented by the equation
x2+2√3xy+3y2−3x−3√3y−4=0, are
View Solution3√2−2√33√2+2√3+3√2+2√33√2−2√3=
View Solutionबहुपद 2x3+x2−5x+2के अन्य शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक 1 और-2 हैं। ज्ञात कीजिए,
View Solution
