k का मान ज्ञात कीजिए , यदि x2+2x+k बहुपद 2x+x3−14x2+5x+6 का एक गुणनखण्ड है दोनों बहुपदो के सभी शून्यक भी ज्ञात कीजिए ।
∵x2+2x+k दिए गए बहुपद का एक गुणनखण्ड होगा , तब विभाजन एल्गोरिथ्म के प्रयोग से शेषफल शून्य होना चाहिए ।
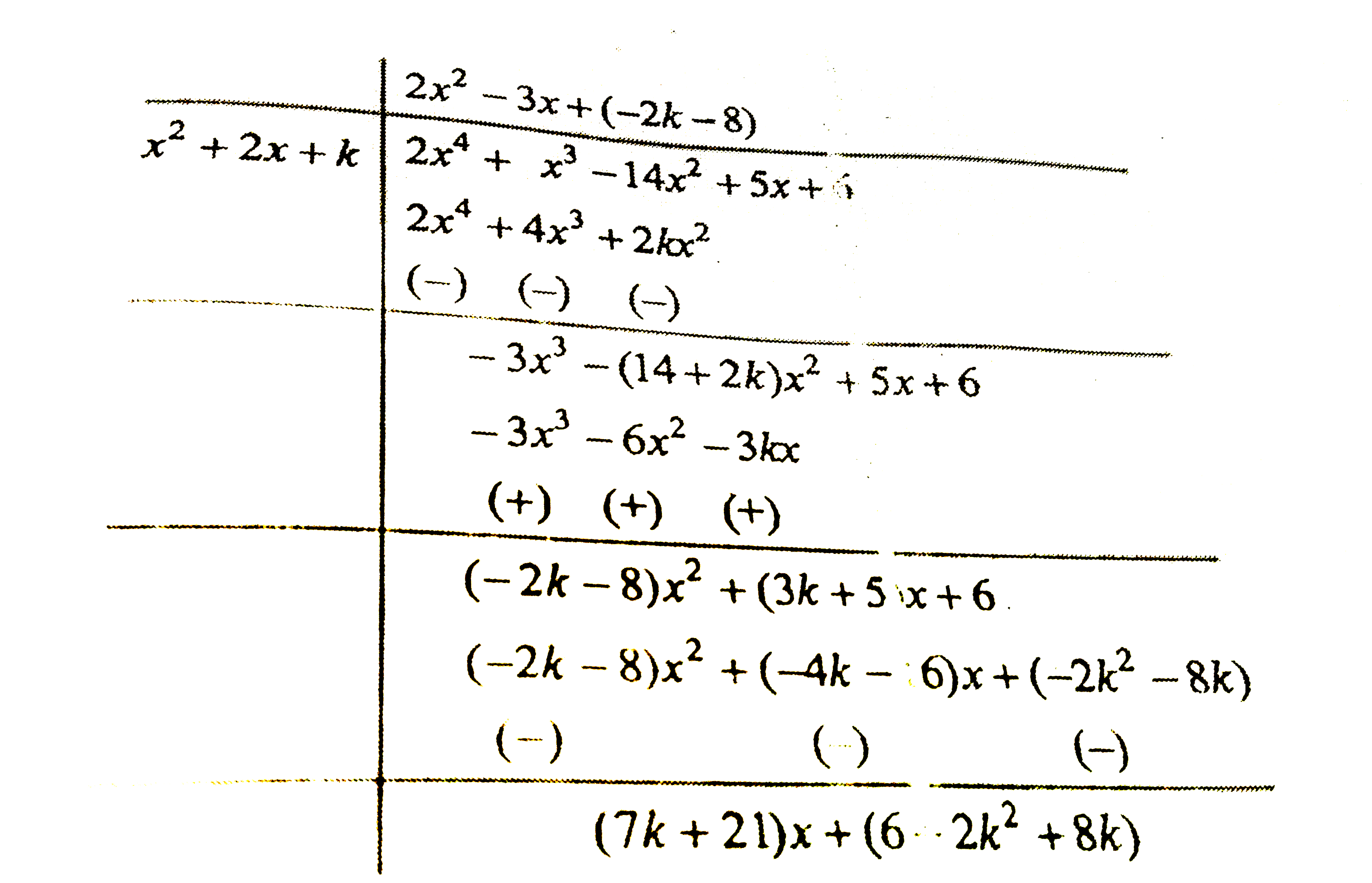
अंत : (7k+21)x+(6+2k2+8k)=0=0,x+0
दोनों पक्षों कि तुलना करने पर ,
7K+21=07k=−21k=−3∣∣
∣
∣
∣
∣
∣∣2k2+8k+6=0k2+4k+3=0k23k+k+3=0k(k+3)+1(K+3)=0(k+3)(k+1)=0
अंत : k =-3 लेने पर शेषफल शून्य होता है ।
∴ विभाजन एल्गोरिथ्म के प्रयोग से ,
2x4+x3−14x2+5x+6=(x2+2x−3)(2x2−3x−2)
=(x2+3x−x−3)(2x2−4x+x−2)
=[x(x+3)−1(x+3)]02x(x−2)+1(x−2)]
=(x+3)(x−1)(x−2)(2x+1)
अंत : बहुपद के शून्यक −3,1,2 और−12 है
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नवाली 2(A)1videos
बहुपद
- BOOK - MANOHAR RAYCHAPTER - बहुपद EXERCISE - प्रश्नावली 2(B)15videos
बहुपद
- BOOK - MANOHAR RAYCHAPTER - प्रोजेक्ट EXERCISE - परीक्षा प्रश्न - पत्र, 201930videos
प्रोजेक्ट
- BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(E)25videos
वास्तविक संख्याएँ
Similar Questions
किसी बहुपद f (x ) ले लिए y =f (x ) के ग्राफ दिए है । प्रत्येक ग्राफ में f (x ) के शून्यको की संख्या कीजिए :

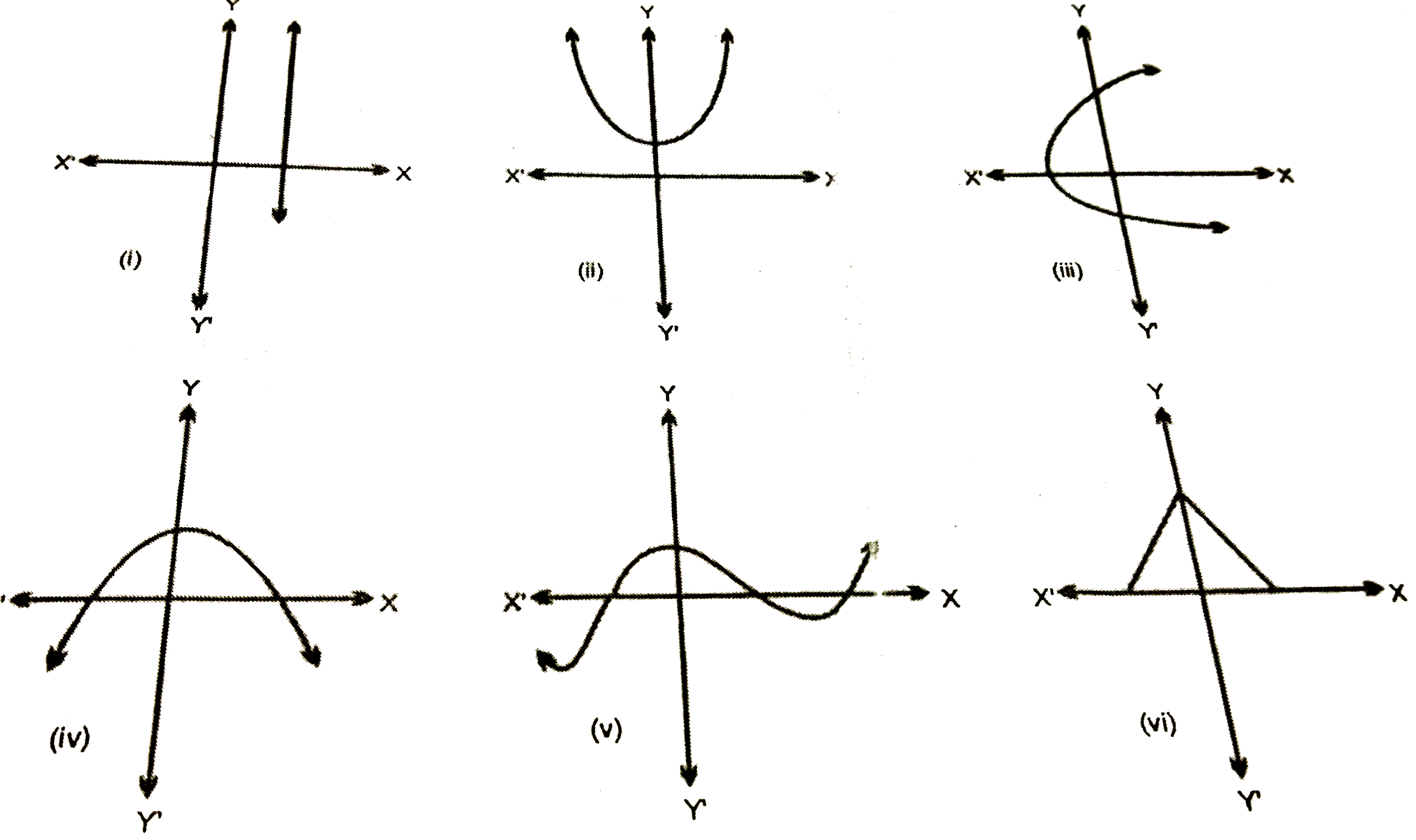
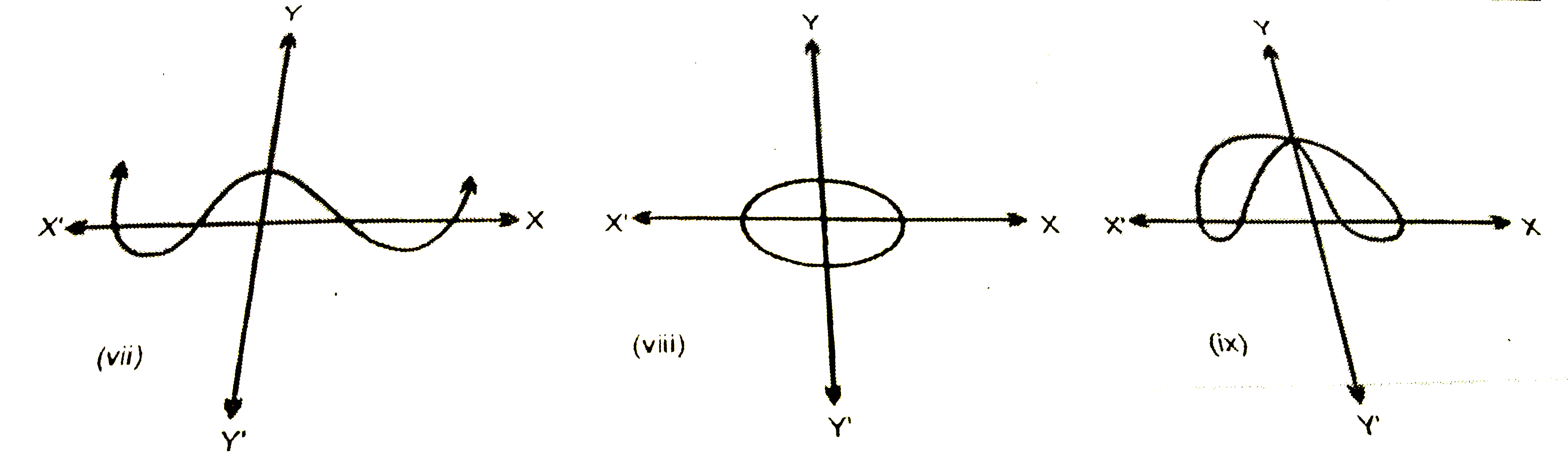 04:37View Solution
04:37View Solutionनिम्न बहुपदो के शून्यको तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए :
(i)x2−2x−8
(ii) 4s2−4s+1
(iii)6x2−3−7x05:02View Solution(क) निम्नलिखित में से कौन- सा ग्राफ द्विघात समीकरण का नहीं है ?
03:39View Solutionनिन्मलिखित में से परिमेय संख्याएँ छाँटकर लिखिए: √3,π3,2273√4,√414 और 2.33
06:11View Solutionयदि 2x+y=1 तो फलन x2y का उच्चिष्ठ मान ज्ञात कीजिए
04:37View Solutionनिम्नलिखित समाकलों का मान ज्ञात कीजिए :
∫x2+1(2x+1)(x2−1)dx03:38View Solutionनिम्नलिखित समाकलों का मान ज्ञात कीजिए :
∫x2+1x4−2x2+1dx01:28View Solution(x−2x2)−3 के प्रसार में x7 का गुणांक ज्ञात कीजिए|
05:17View Solution1−2x+3x2ex के प्रसार में x5 का गुणांक ज्ञात कीजिए|
03:45View Solutionपरवलय y=x2−2x+3 का शीर्ष, नाभि, अक्ष तथा नियता का समीकरण ज्ञात कीजिए।
06:23View Solutionlimx→∞sinxx का मान ज्ञात कीजिए ।
07:10View Solution1+cosec2x का न्यूनतम मान ज्ञात कीजिए।
01:31View Solutionयदि y=1−cos2x1+cos2x है तो dydx का मान ज्ञात कीजिए।
02:51View Solutionx के मानों का वह सम्मुच्य ज्ञात कीजिए, जिसके लिए
2x2x2+5x+2>1x+101:53View Solution∫π−π2x(1+sinx)1+cos2xdx का मान ज्ञात कीजिए।
01:53View Solutionचरों के दिए गए मान पर निचे दिए गए प्रत्येक बहुपद का मान ज्ञात कीजिए :
y=2 पर p(x)=3y2−4y+4 का मान01:57View Solution

