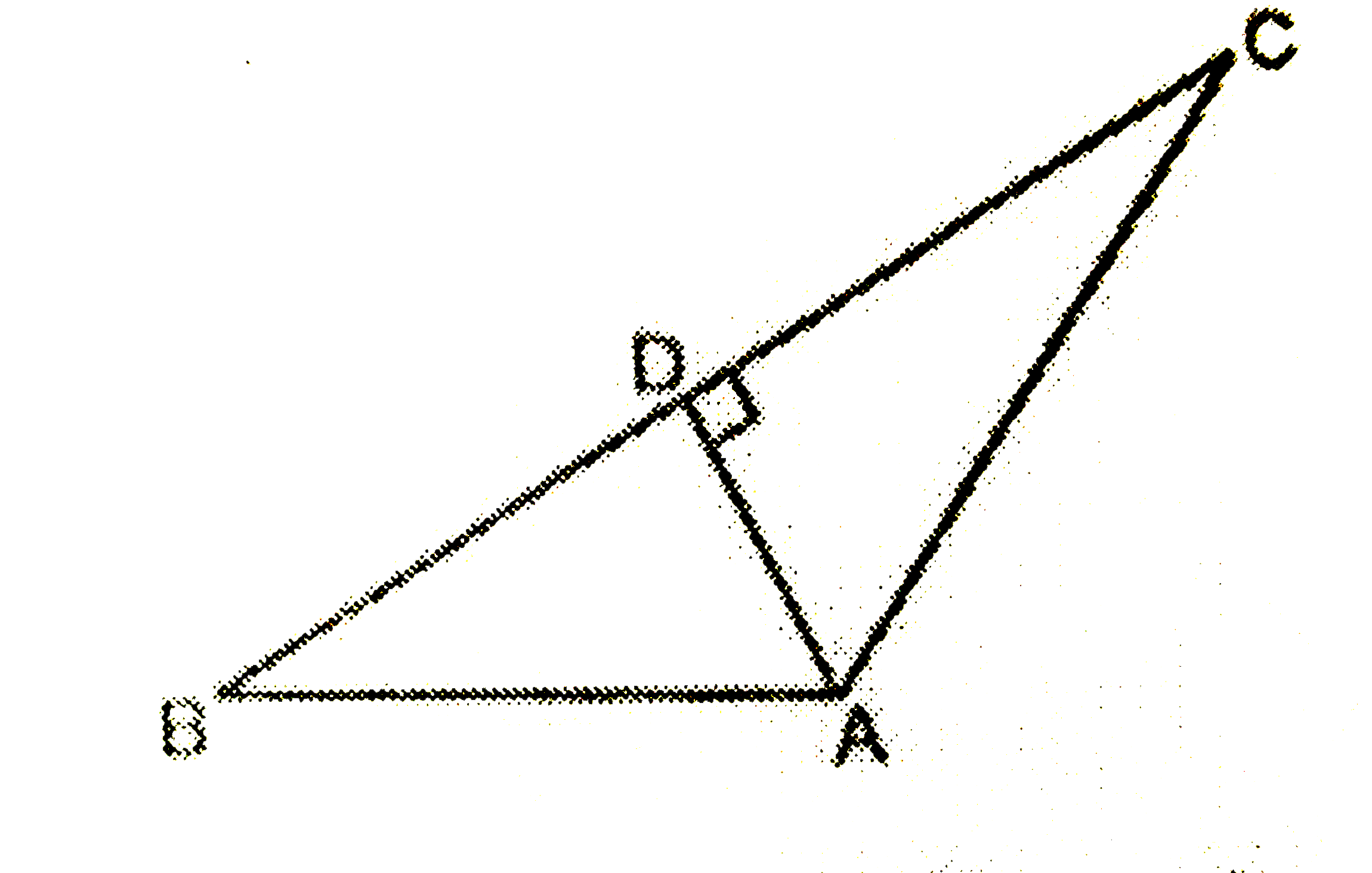
दी हुई आकृति में AD⊥BC है । सिद्ध कीजिए कि AB2+CD2=BD2+AC2 है ।
ΔADC से , AC2=AD2+CD2 . . . (1)
पुनः ΔADB से , AB2=AD2+BD2 . . . (2)
सम्बन्ध (2) में से (1) को घटाने पर
AB2−AC2=BD2−CD2
AB2+CD2=BD2+AC2.
Topper's Solved these Questions
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - उदाहरण
1 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6(A)
2 Videos
- त्रिकोणमिति के कुछ अनुप्रयोगBOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय
2 Videos
- दो चार वाले रैखिक समीकरण युग्मBOOK - MANOHAR RAYCHAPTER - दो चार वाले रैखिक समीकरण युग्मEXERCISE - प्रश्नावली 3(I)
20 Videos
Similar Questions
निम्न आकृति में ∠P ज्ञात कीजिए ।

View Solutionनिम्नलिखित युग्मों के दो भिन्न - भिन्न उदाहरण दीजिए :
(i) समरूप आकृतियाँ
(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।

View Solutionसमीकरण 8x+5y=11 को संतुष्ट करने वाले बिन्दु के निर्देशांक है :
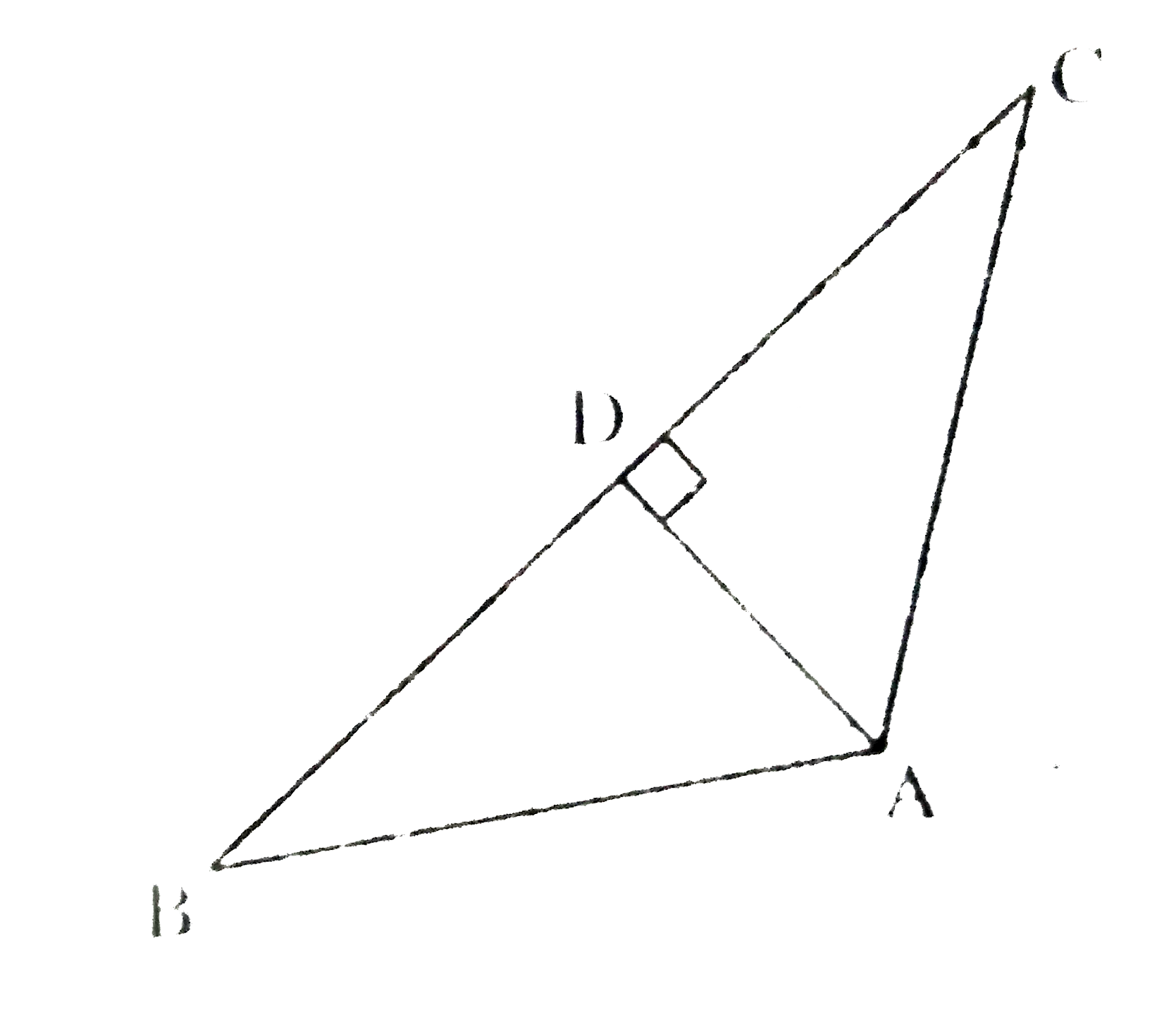
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionABCD is a trapezium in which AB||CD then AC^(2)+BD^(2) is equal to
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View Solutionचित्र में BD=DC है । सिद्ध कीजिए- AB2+CD2=BD2+AC2
View Solutionएक △ABC में, यदि AD, BC के लंबवत है तो सिद्ध कीजिए कि
(i) AB2+CD2=AC2+BD2
(ii) AB2−BD2=AC2−CD2
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionयदि p मूलबिंदु से रेखा xa+yb=1 पर लम्ब कि लम्बाई है तथा a2,p2,b2 समान्तर श्रेढी में है , तब सिद्ध कीजिए कि a4+b4=0
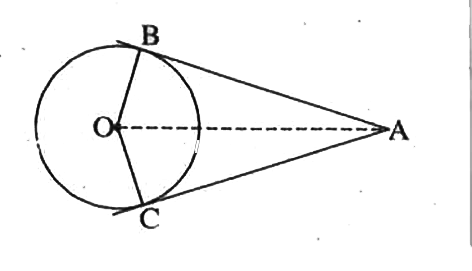
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में वर्धमान है ।
f(x)=logsinx,x∈(0,π2)
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=x2−2x+3,x<1
View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए हुए अन्तराल में ह्रासमान है -
f(x)=x2−2x+3,x<1
View Solution
