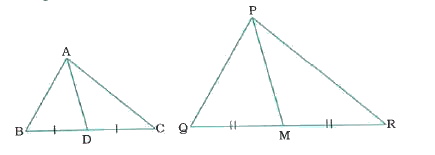
AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
Step by step video, text & image solution for AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि DeltaABC~DeltaPQR है । सिद्ध कीजिए कि (AB)/(PQ)=(AD)/(PM) है । by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6(D)
14 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (D )
1 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (C )
2 Videos
- त्रिकोणमिति के कुछ अनुप्रयोगBOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय
2 Videos
- दो चार वाले रैखिक समीकरण युग्मBOOK - MANOHAR RAYCHAPTER - दो चार वाले रैखिक समीकरण युग्मEXERCISE - प्रश्नावली 3(I)
20 Videos
Similar Questions
दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं । इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
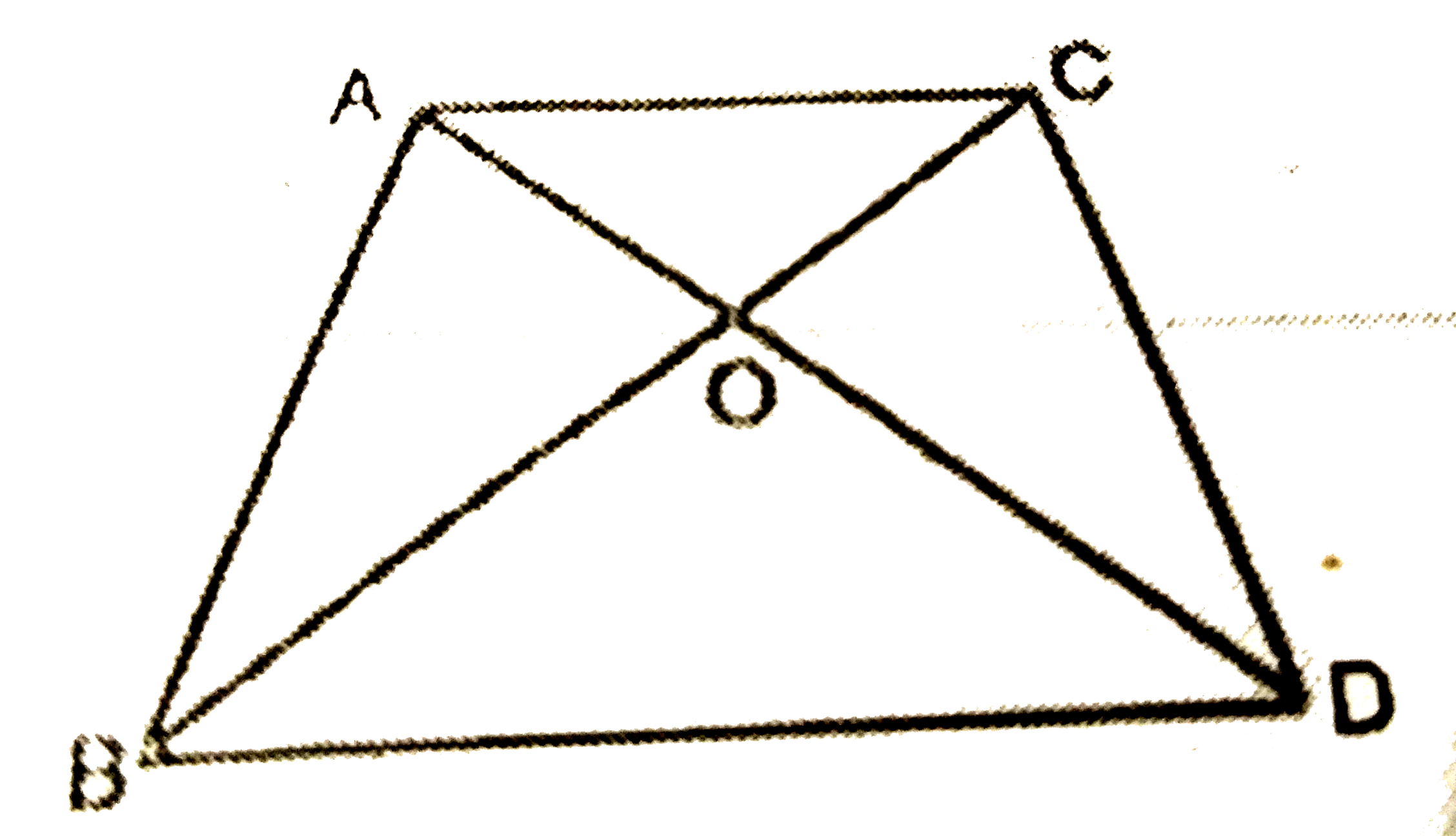
View Solutionदी गयी आकृति में , एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं । यदि AD , BC को O पर प्रतिच्छेद करे , तो दर्शाइए कि :
ar(ΔABC)ar(ΔDBC)=AODO.
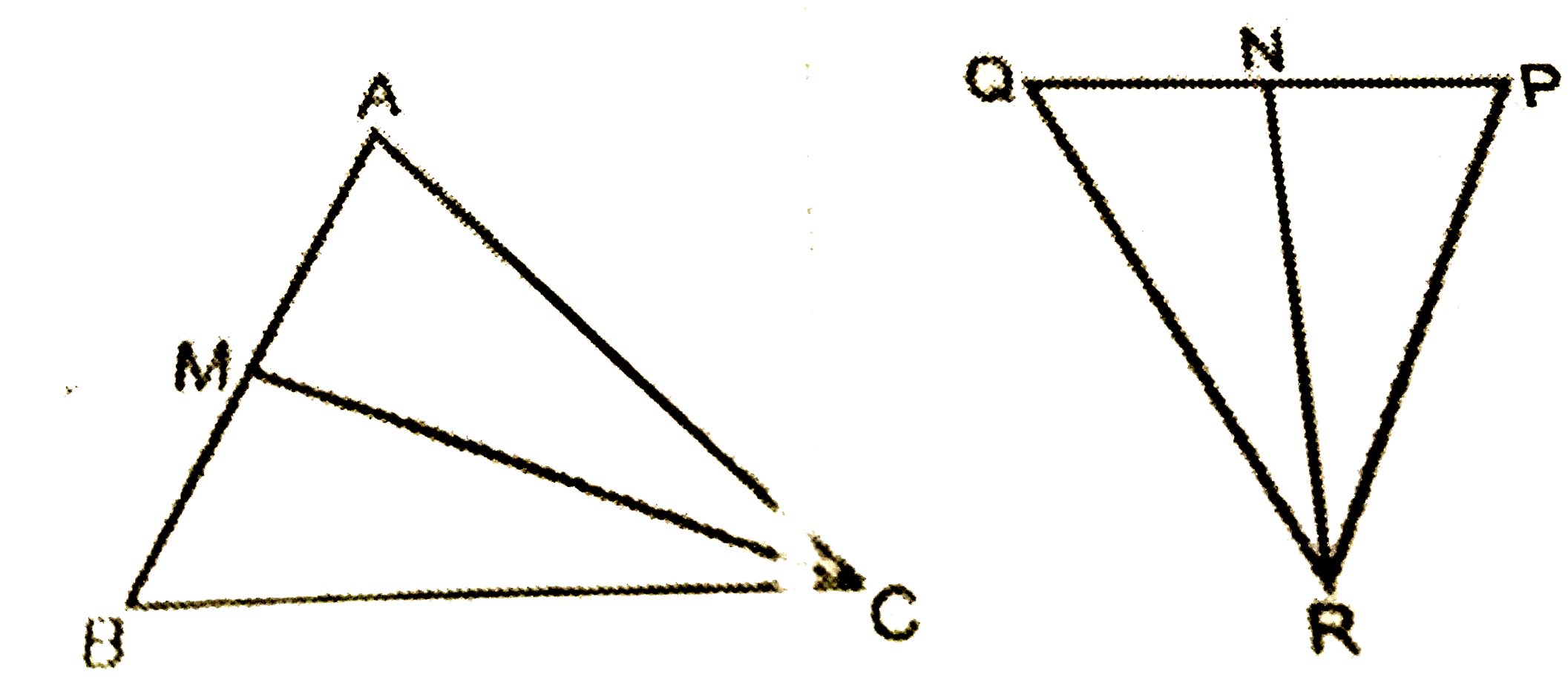
View Solutionदी हुई आकृति में CM और RN क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं । यदि ΔABC~ΔPQR है तो सिद्ध कीजिए :
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(iii) ΔCMC~ΔRNO.
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।

View Solutionसमीकरण 8x+5y=11 को संतुष्ट करने वाले बिन्दु के निर्देशांक है :
View SolutionAD और PM त्रिभुजों ABC और PQR कि क्रमशः मध्यिकाएँ है जबकि ΔABC~ΔPQR है सिद्ध कीजिए कि ABPQ=ADPM है
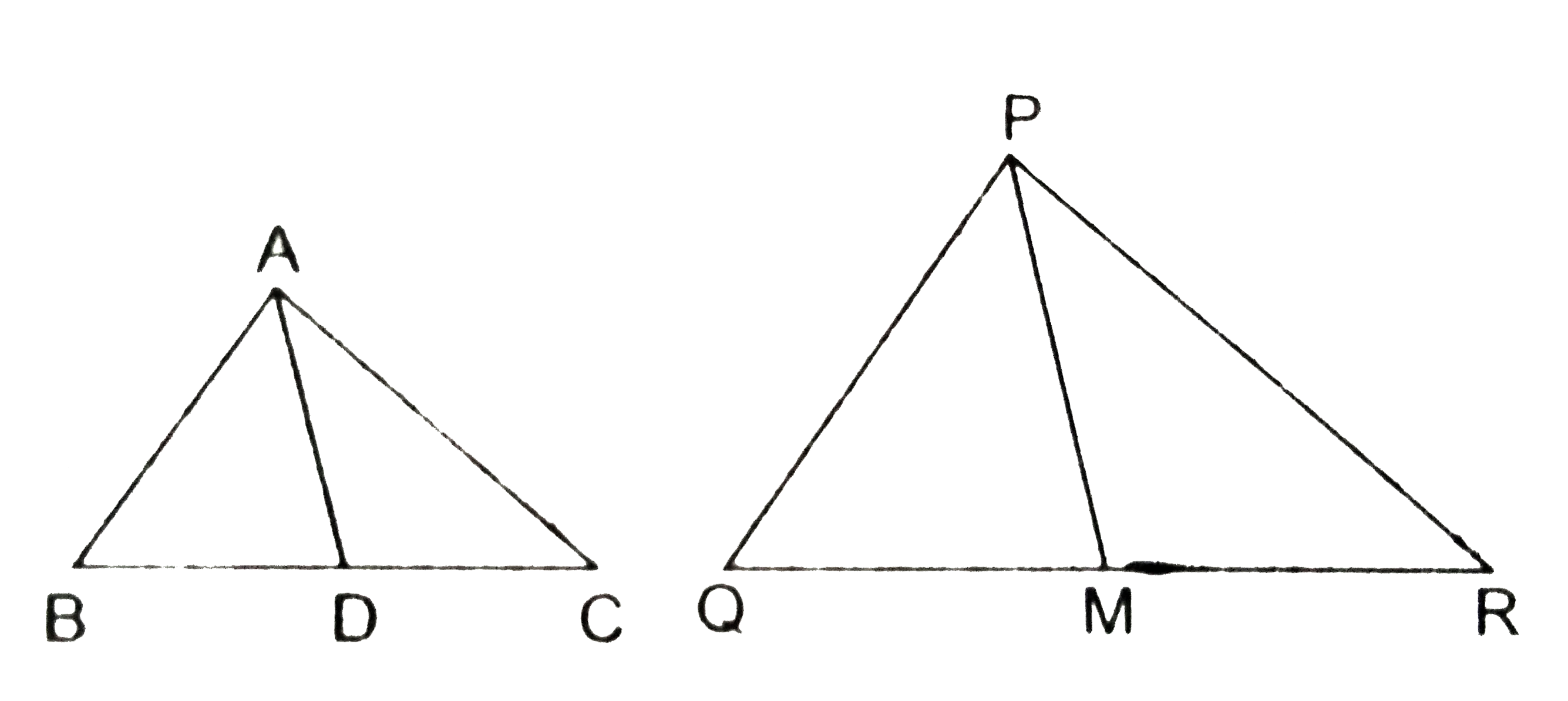
View Solutionएक त्रिभुज ABC की भुजाएं AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है। दर्शाइए कि ΔABC~ΔPQR है।
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View Solutionयदि AD और PM ΔABCऔरΔPQR की क्रमशः मध्यिकाएँ है , और जहाँ ΔABC~ΔPQR सिद्ध करें कि
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
View SolutionIf AD and PM be two medians of ΔABC and ΔPQR respectively, where ΔABC~ΔPQR, then prove that ABPQ=ADPM.
View SolutionΔABC की भुजाएँ AB और BC और माध्यिका AD क्रमशः ΔPQR की भुजाओं PQ और QR माध्यिका PM के बराबर है। सिद्ध कीजिए कि त्रिभुज ABC और PQR सर्वांगसम है।
View Solutionsides AB and BC and median AD of a triangle ABC are respectively proportional to side PQ and QR median PM of ΔPQR (see Fig ). Show that ΔABC~ΔPQR
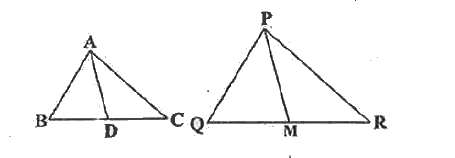
View SolutionIf Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIf AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
View Solution
