एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC=∠BAC है । दर्शाइए कि CA2=CB⋅CD है ।
Step by step video, text & image solution for एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि angleADC=angleBAC है । दर्शाइए कि CA^(2)=CB*CD है । by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6(D)
14 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (D )
1 Videos
- त्रिभुज BOOK - MANOHAR RAYCHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6 (C )
2 Videos
- त्रिकोणमिति के कुछ अनुप्रयोगBOOK - MANOHAR RAYCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोगEXERCISE - लघु उत्तरीय
2 Videos
- दो चार वाले रैखिक समीकरण युग्मBOOK - MANOHAR RAYCHAPTER - दो चार वाले रैखिक समीकरण युग्मEXERCISE - प्रश्नावली 3(I)
20 Videos
Similar Questions
दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं । इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
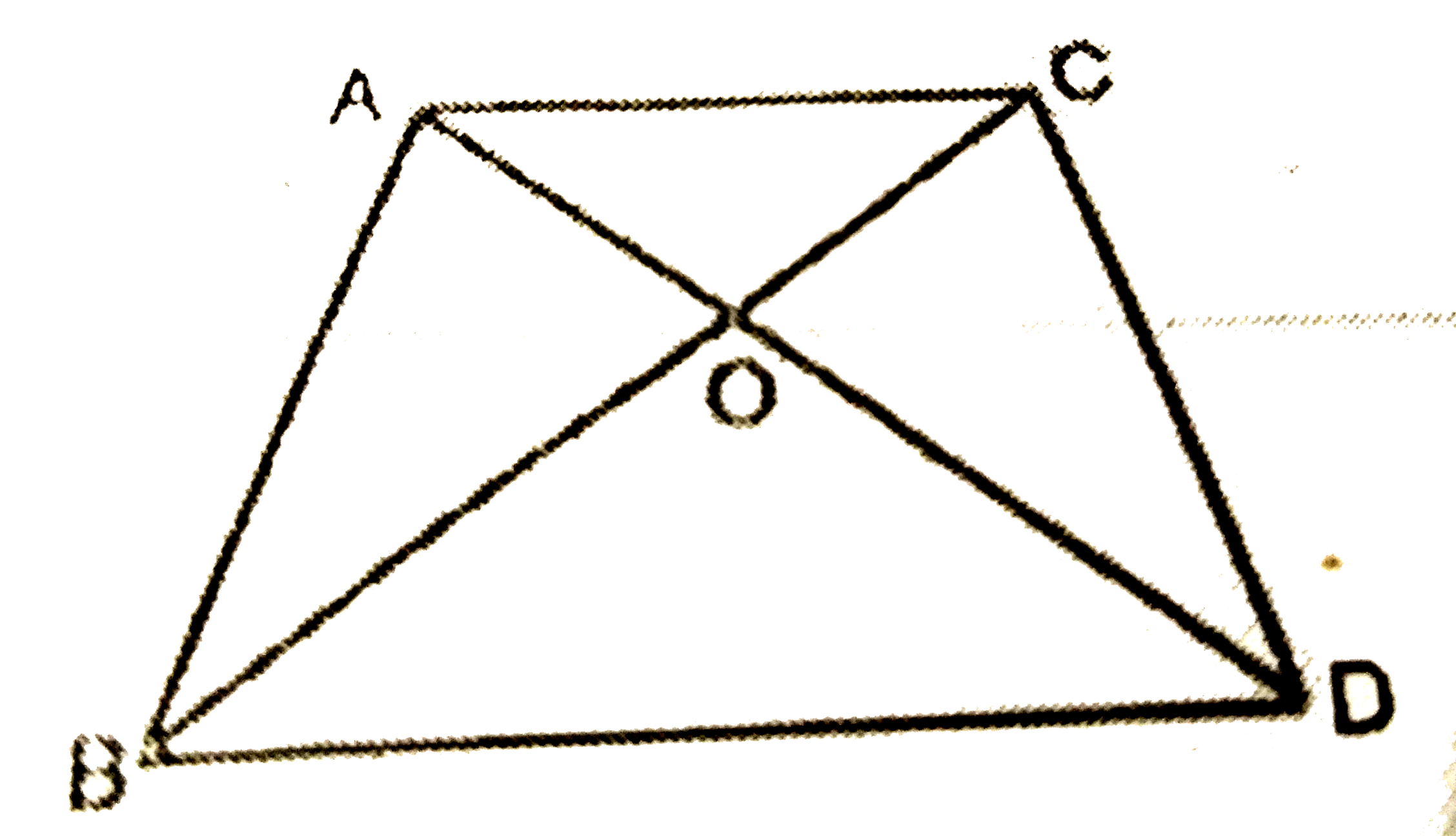
View Solutionदी गयी आकृति में , एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं । यदि AD , BC को O पर प्रतिच्छेद करे , तो दर्शाइए कि :
ar(ΔABC)ar(ΔDBC)=AODO.
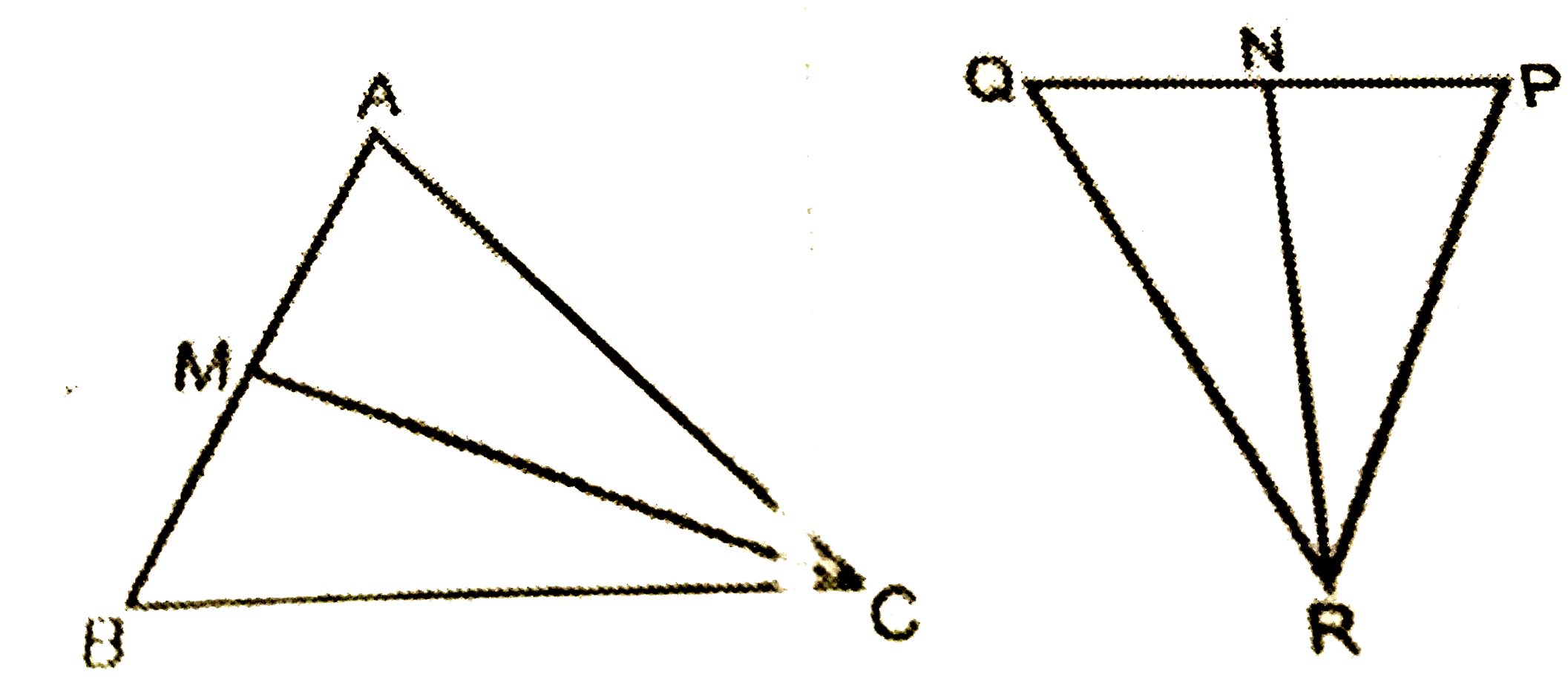
View Solutionदी हुई आकृति में CM और RN क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं । यदि ΔABC~ΔPQR है तो सिद्ध कीजिए :
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(iii) ΔCMC~ΔRNO.
View Solutionएक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधर : खड़ा हैं । टॉवर के ठीक सामने दूसरे के एक अन्य बिंदु से टॉवर शिखर का उन्नयन कोण 60∘ है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 30∘ है (देखिए आकृति) । टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए ।

View Solutionसमीकरण 8x+5y=11 को संतुष्ट करने वाले बिन्दु के निर्देशांक है :
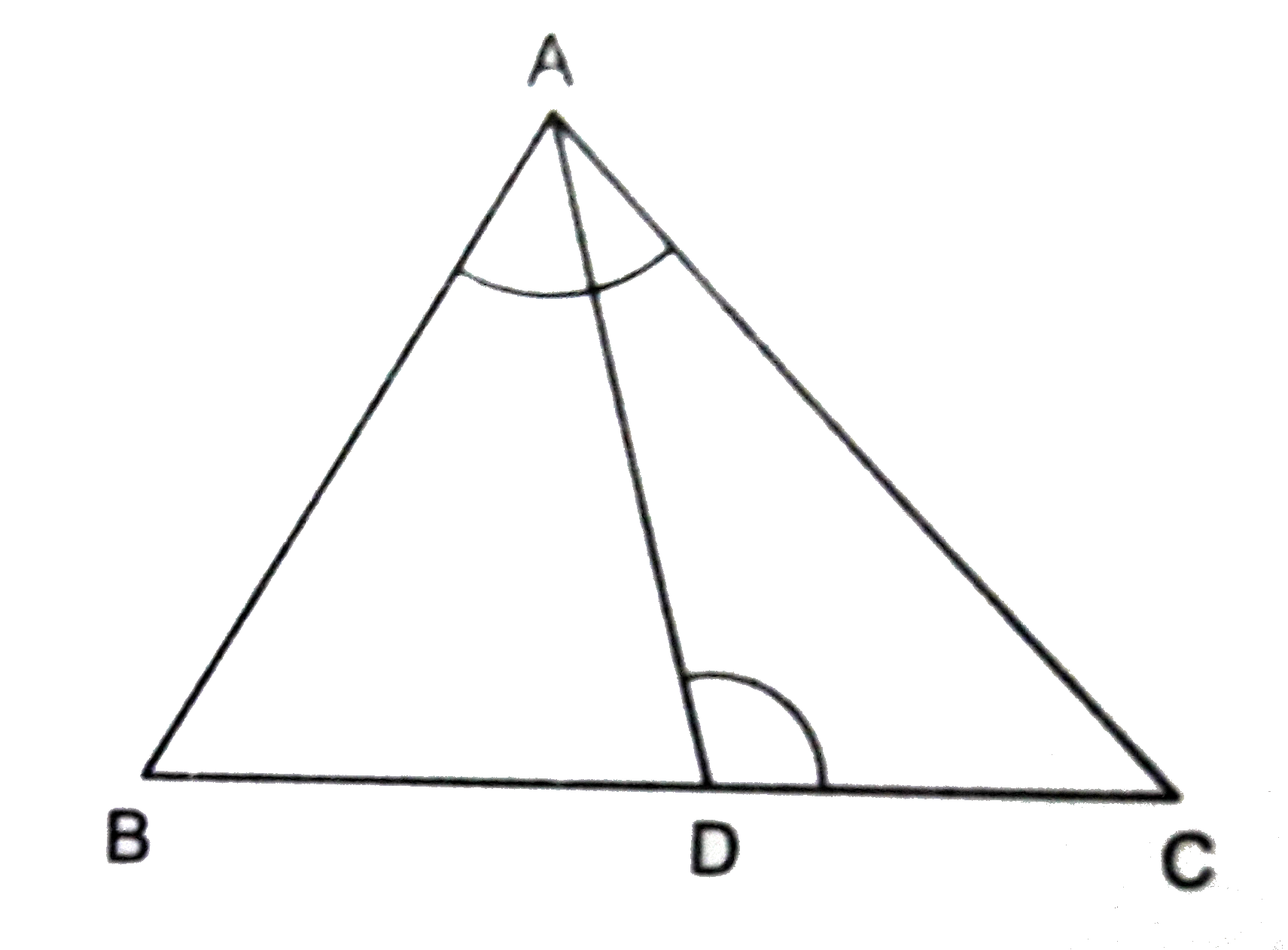
View Solutionचित्र 1 में त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार है कि ∠ADC=∠BAC, तो सिद्ध कीजिए CACD=CBCA
View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC . Show that CA2 = CB. CD.
View SolutionIn △ABC, D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, CB = 8 cm, then CD is equal to:
त्रिभुज ABC में भुजा BC पर D बिंदु इस प्रकार स्थित है कि ∠ADC=∠BAC होता है। यदि CA = 12 सेमी, CB = 8 सेमी, तो CD निम्नलिखित में किसके बराबर है?
View Solution
