एक समलम्ब चतुर्भुज है जिसमें तथा भुजा AD का मध्य बिंदु है। यदि BC पर कोई बिंदु इस प्रकार हो कि तो सिद्ध कीजिए
ज्ञात है: समलम्ब चतुर्भुज ABCD में भुजा का मध्य बिंदु है और है।
सिद्ध करना है:
रचना को से मिलाया जिसने को पर काटा।
उपपत्ति: (ज्ञात है)...............1
किंतु (ज्ञात है).....2
समीकरण 1 तथा 2 से
………3
……….4
में का मध्य बिंदु है (ज्ञात है)
[समीकरण 4 से ]
का मध्य बिंदु है। ..............5
( की एक भुजा के मध्य बिंदु से दूसरी भुजा के समांतर खींची जाने वाली रेखा तीसरी भुजा के समांतर होती है।)
……….6
पुन: में का मध्य बिंदु है। [समीकरण 5 से]
तथा [ ]
का मध्य बिदुं है।
…………7
( की एक भुजा के मध्य बिंदु से दूसरी भुजा के समांतर खींची जाने वाली रेखा तीसरी भुजा के समांतर होती है।)
समीकरण 6 तथा 7 को जोड़ने पर
यही सिद्ध करना था।

Topper's Solved these Questions
Similar Questions
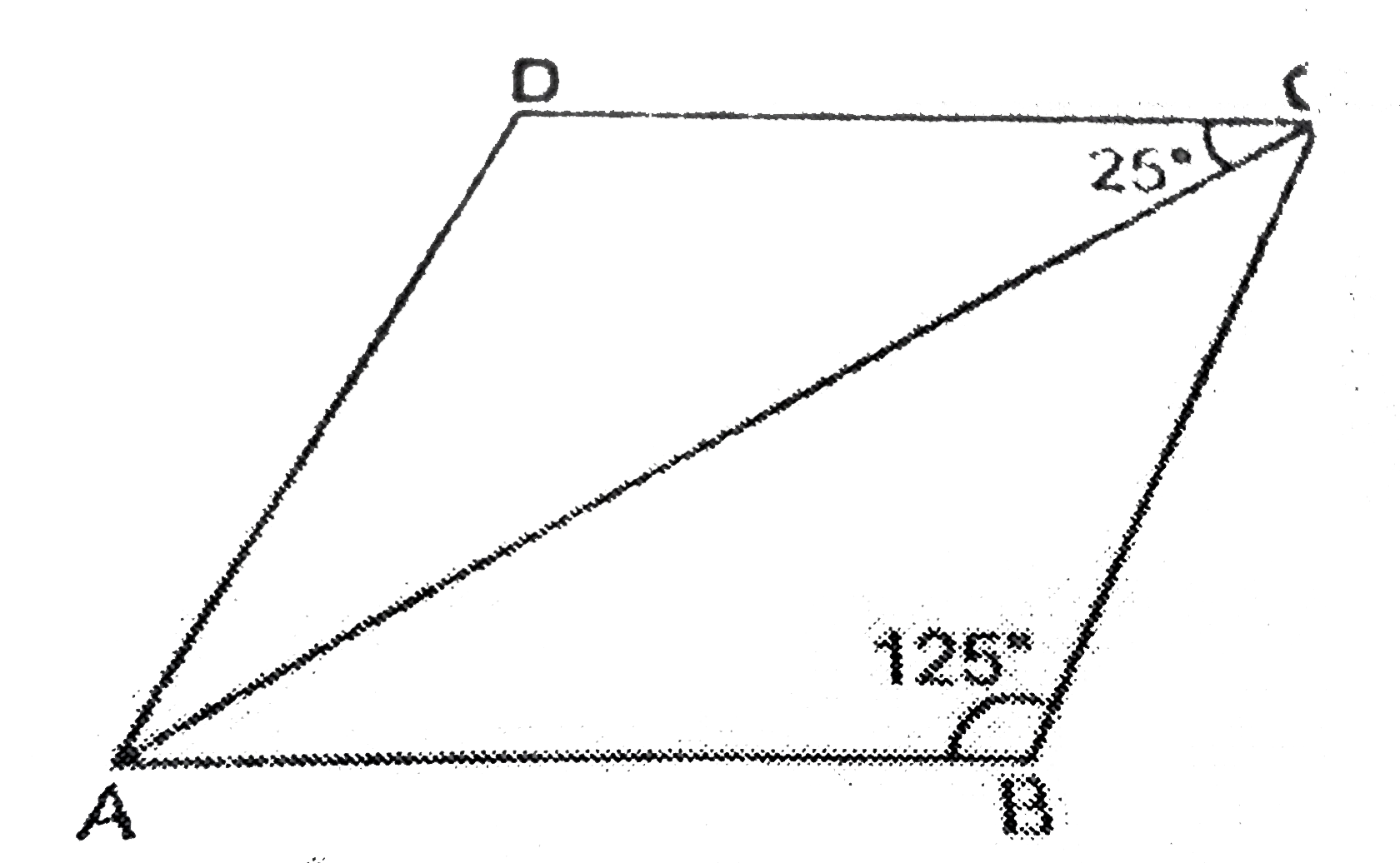
चित्र में ABCD एक समान्तर चतुर्भुज है। यदि ∠ABC=125∘ और ∠DCA=25∘ तो ∠DAC ज्ञात कीजिए।
View Solutionचतुर्भुज ABCD में ∠A=∠C तथा ∠B=∠D हैं। सिद्ध कीजिए ABCD एक समांतर चतुर्भुज है।
View Solutionचित्र में AB>AC है सिद्ध कीजिएः की AB>AD

View Solutionरेखाखण्ड AB अक्षो के बीच इस प्रकर गति करता है की A सदैव Y-अक्ष पर तथा B सदैव X- अक्ष पर हो । रेखाखण्ड AB पर एक बिंदु P इस प्रकार है की PA =a और PB =b यदि AB=a+b हो , तो बिंदु P का बिन्दुपथ ज्ञात कीजिये
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View SolutionABCD is a trapezium in which AB || DC and E is the mid-point of AD. If F be a point on BC such that EF || DC, then prove that EF=12(AB+DC).
View Solutionयदि AB और CD असमान्तर रेखा हो ,तो इनसे समान दुरी पर रहने वाले बिंदु P का बिन्दुपथ होगा -
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View SolutionAB एक ऊर्ध्वाधर खंभा है, जिनका A सिरा जमीन पर है | C, AB का मध्य-बिंदु है और P जमीन पर एक बिंदु है | BC, बिंदु P पर β कोण बनता है | यदि AP = nAB हो, तो tanβ का मान है |
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
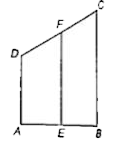
View SolutionIn trapezium ABCD, AB || CD and E is the midpoint of AD. A line drawn through E and parallel to AB intersects BC at F. Prove that F is the midpoint of BC and EF=12(AB+CD).
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
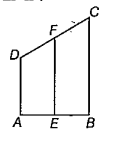
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View Solution
