त्रिज्या R1 का एकसमान आवेश घनत्व का गोलाकार आवेश मूल बिंदु O पर केंद्रित है इस वितरण में त्रिज्या R2 तथा P पर केंद्रित एक गोलाकार गुहिका जहाँ दूरी OP a=R1−R2 है बनाई जाती है यदि गुहिका के अंदर स्थित ˆr पर विधुत क्षेत्र ˆE है तब सही कथन है
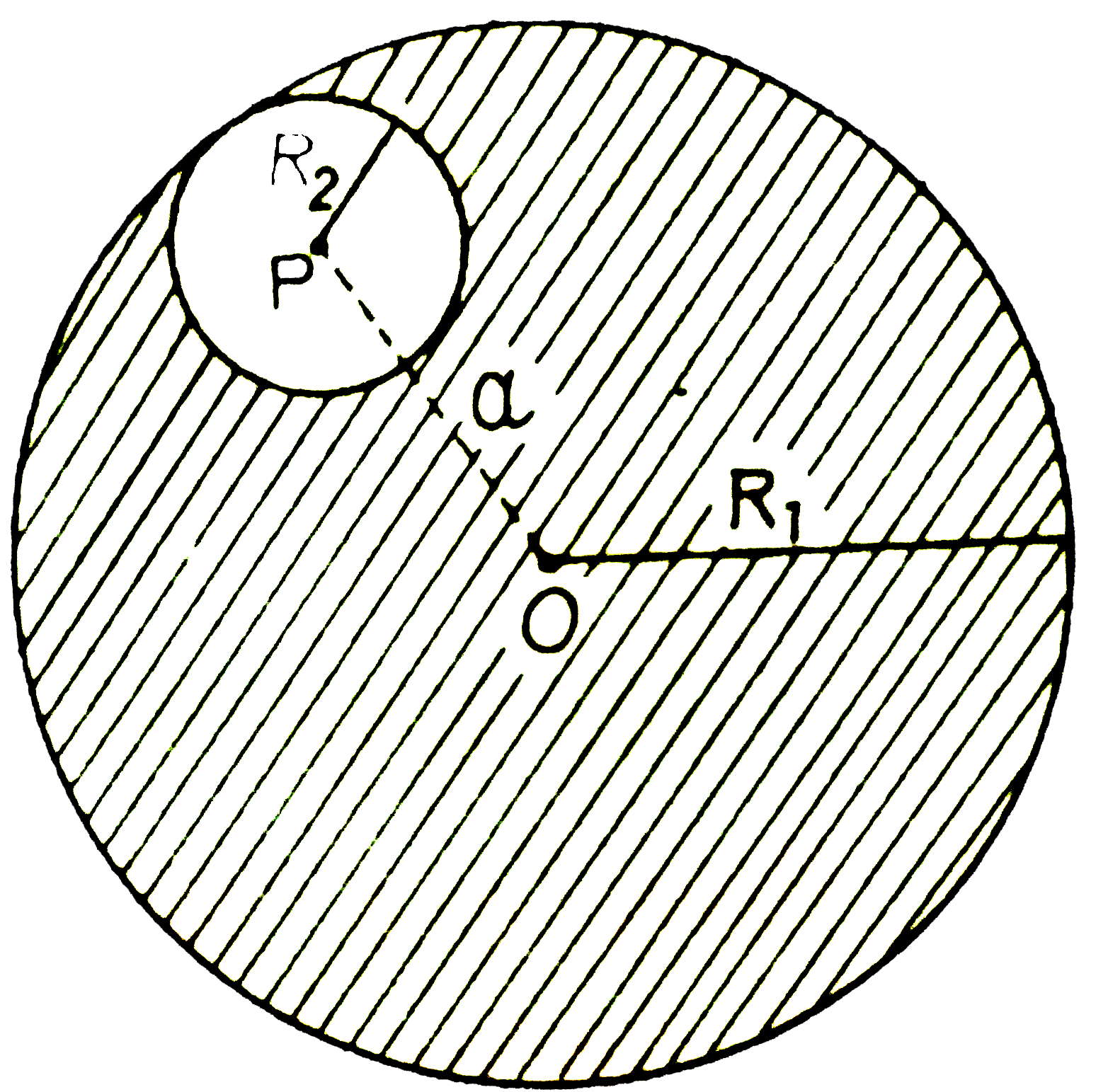
→E एकसमान है इसका परिमाण R2 निर्भर नहीं करता है परन्तु इसकी दिशा →r निर्भर करती है
→E एकसमान है इसका परिमाण R2 पर निर्भर करता है परन्तु इसकी दिशा →r पर निर्भर करती है
→E एकसमान है इसका परिमाण a पर निर्भर नहीं करता है परन्तु इसकी दिशा →a पर निर्भर करती है
→E एकसमान है एव परिमाण तथा दिशा दोनों →a पर निर्भर करते है
The correct Answer is:D
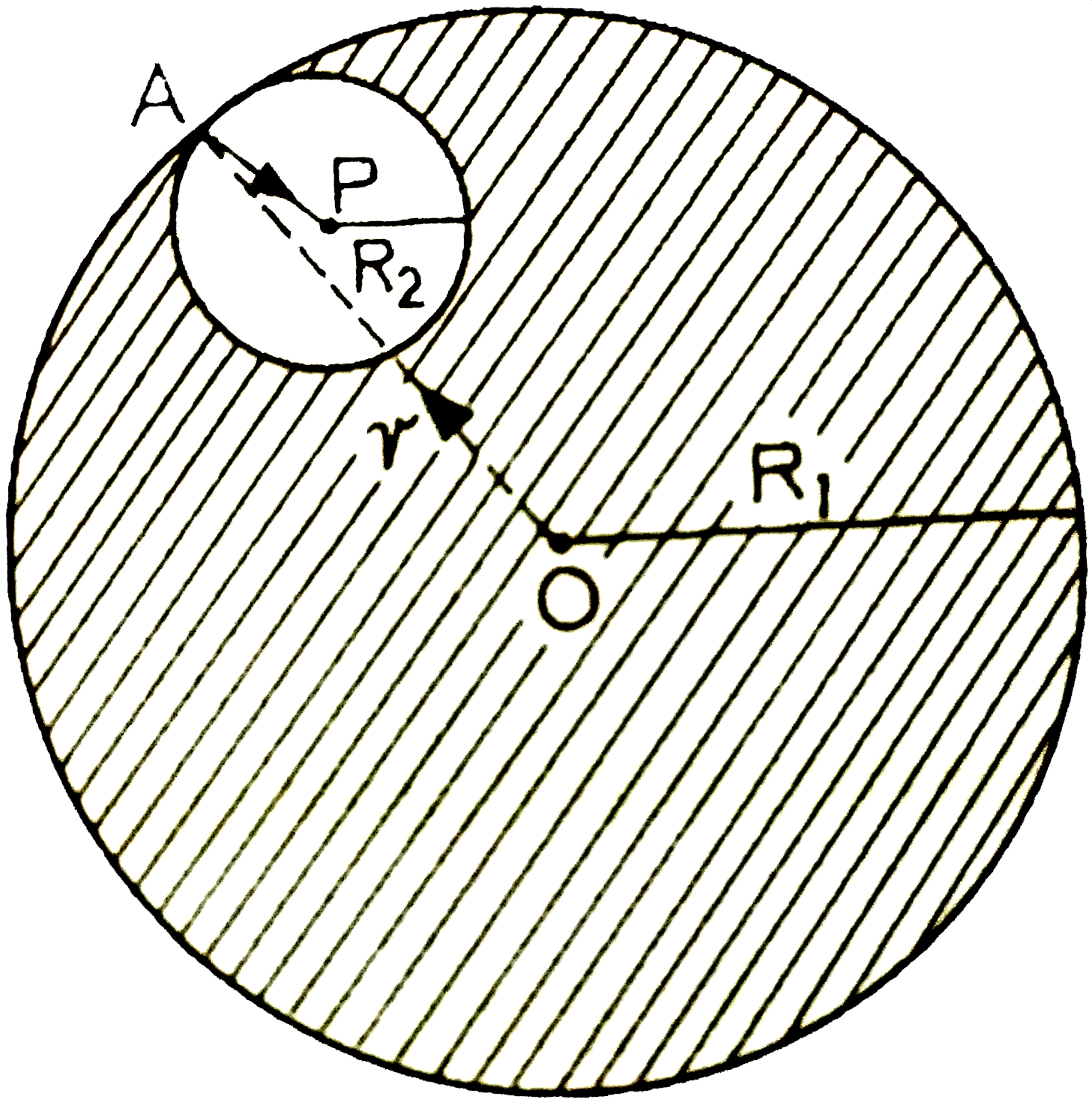
E=→E1+→E2
=ρ3ε0→OA+ρ3ε0→AP
=ρ3ε0(→OA+→AP)=ρ3ε0→OP
=ρ3ε0→a
झा ρ आवेश घनत्व है इस प्रकार कथन (d) सही है
Topper's Solved these Questions
- वैधुत फ्लेक्स तथा गौस की प्रमेय BOOK - NOOTAN HINDICHAPTER - वैधुत फ्लेक्स तथा गौस की प्रमेय EXERCISE - आंकिक
16 Videos
- वैधुत चालनBOOK - NOOTAN HINDICHAPTER - वैधुत चालनEXERCISE - वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार )
24 Videos
- वैधुत विभव BOOK - NOOTAN HINDICHAPTER - वैधुत विभव EXERCISE - विविध प्रतियोगी परीक्षाओ के लिए (वस्तुनिष्ठ प्रकार प्रश्न एकल उत्तर प्रकार)
17 Videos
Similar Questions
एक आवेश q एक घन के केंद्र पर स्थित है तो घन के किसी भी पृष्ठ से आने वाला वैधुत फ्लक्स होगा -
View Solutionएक राशि X , व्यंजक ε0LΔVΔt द्वारा व्यक्त की जाती है , जहाँ ε0 निर्वात की विधुतशीलता है , L लम्बाई है , ΔV विभवान्तर है तथा Δ समयान्तराल है । X का विमीय सूत्र वही है , जो कि है :
View Solutionएक आवेश Q लम्बाई L की छड़ AB के अनुदिश एकसमान रूप से वितरित है जैसा कि चित्र में दिखाया गया है । एक बिंदु O पर जो सिरे A से L दूरी पर है , वैधुत विभव है :

View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solution
