Question

चित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं। कण की कुल ऊर्जा कोटि-अक्ष पर क्रास द्वारा निर्देशित की है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए , यदि कोई हैं तो, जिनमे दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक संदर्भों के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों।

Explanation

कण की सम्पूर्ण ऊर्जा
`K+U`
जहाँ K कण की गतिज ऊर्जा तथा U स्थितिज ऊर्जा है। यहाँ पर ध्यान रखा जाना चाहिए कि किसी भी वस्तु की गतिज ऊर्जा K सदैव शून्य या धनात्मक ही जो सकती हैं परन्तु ऋणात्मक किसी भी परिस्थिति में नहीं
(`K=(1)/(2)mv^(2), m ne -ve, v` ऋणात्मक हो सकता है परन्तु `v^(2)` सदैव घनात्मक होगा । अतः K या तो शून्य या फिर धनात्मक ही होगा )।
अब चूँकि गतिज ऊर्जा ऋणात्मक नहीं हो सकती, अतः समीकरण `E = K + U` के अनुसार स्थितिज ऊर्जा U का मान सम्पूर्ण ऊर्जा E से कभी भी अधिक नहीं हो सकता । अतः निर्णायक रूप में कण उन क्षेत्रों में कदापि नहीं पाया जा सकता जिनमे गतिज ऊर्जा ऋणात्मक हो
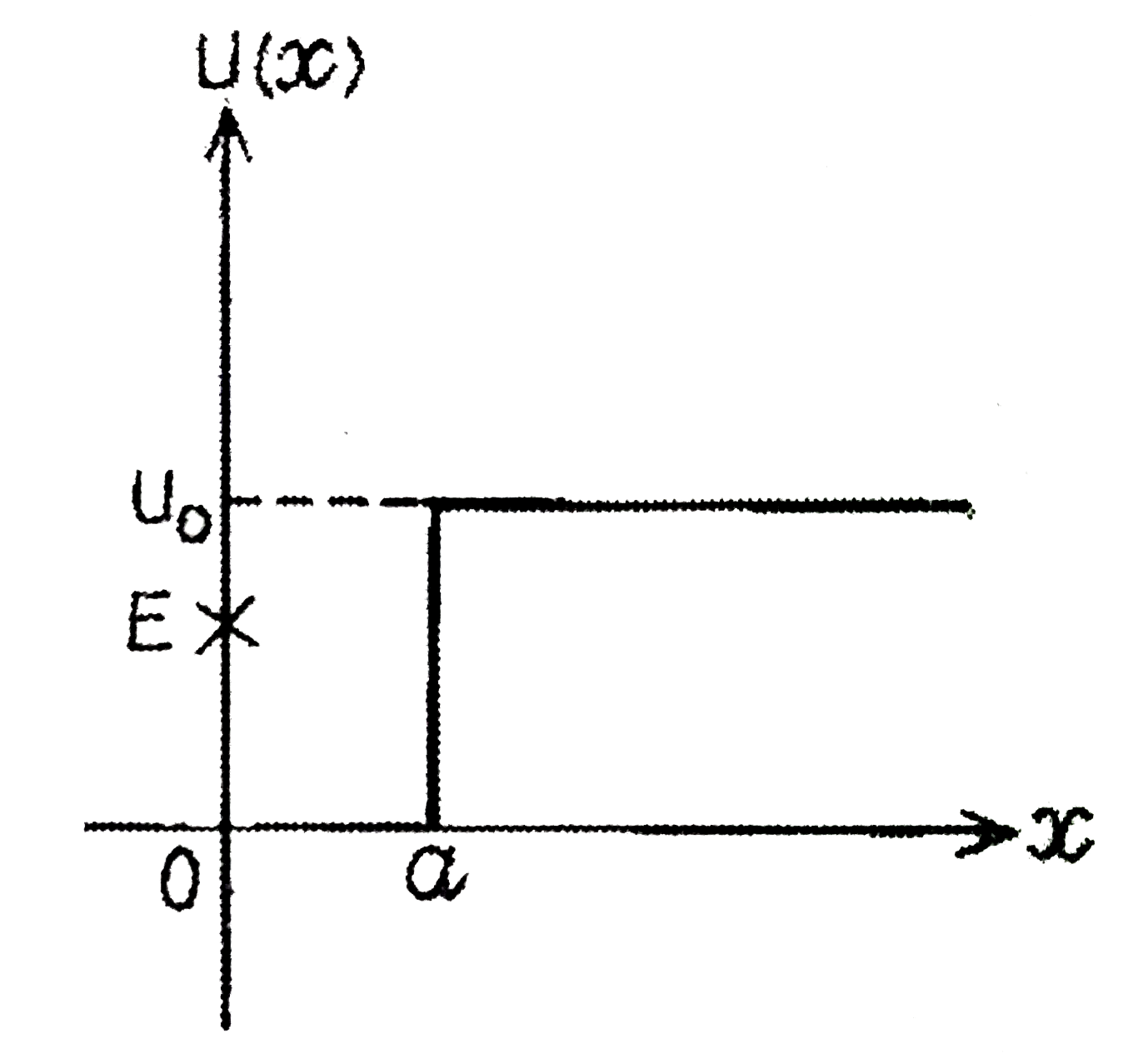
चित्र (a ) में x gt a क्षेत्र में वस्तु की स्थितिज ऊर्जा `U=U_(0)` जो कि सम्पूर्ण ऊर्जा E से अधिक है। इस प्रकार समीकरण `K = E - U` के अनुसार इस परिस्थिति में गतिज ऊर्जा को ऋणात्मक होना चाहिए जो कि सम्भव नहीं है। अतः क्षेत्र x gt a में कण को नहीं पाया जा सकता । अथवा x gt a में कण अस्तित्व में नहीं होगा ।
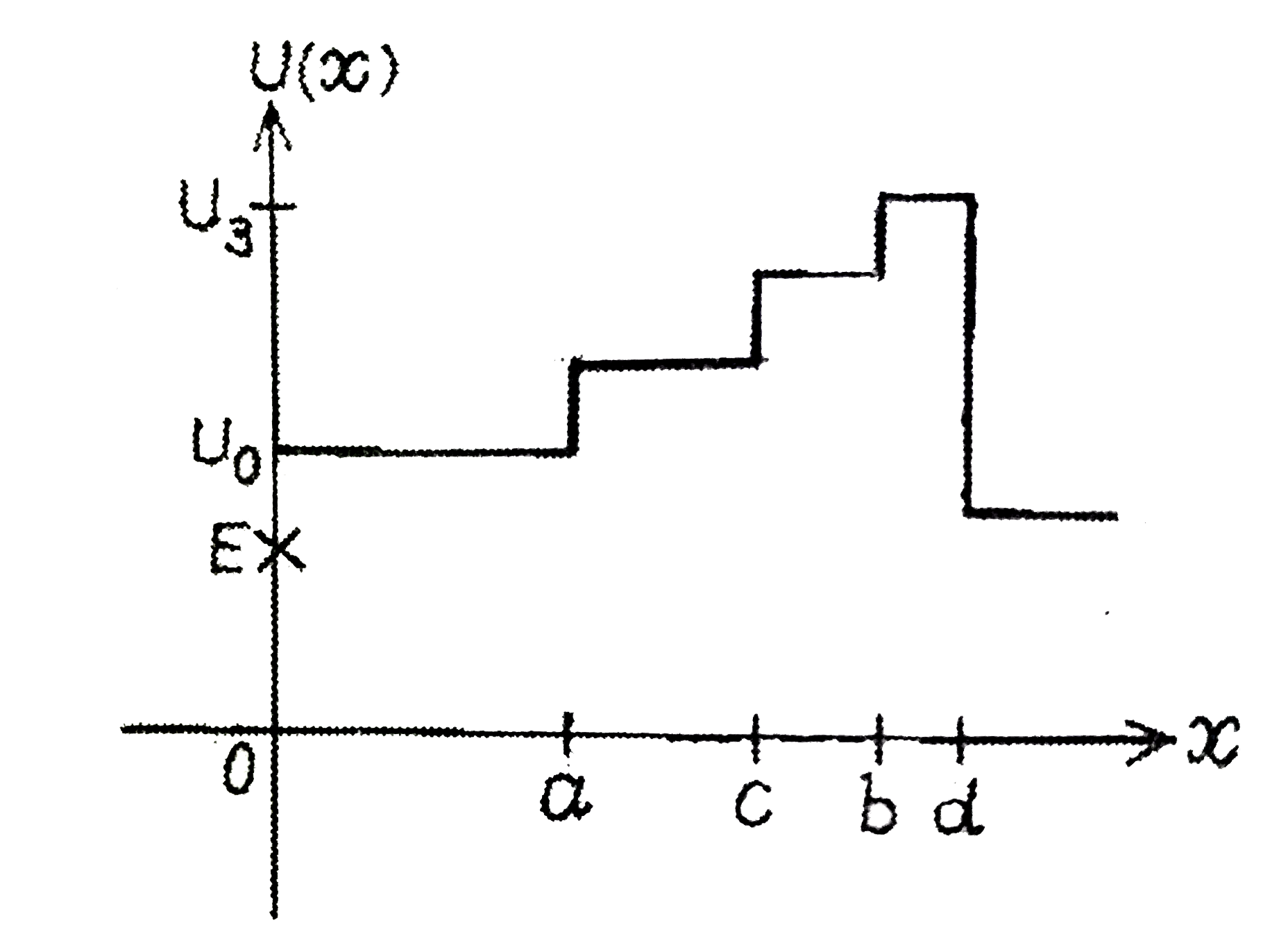
चित्र (b ) में कण की स्थितिज ऊर्जा U gt E , अतः इस क्षेत्र में वस्तु की गतिज ऊर्जा ऋणात्मक होनी चाहिए जो कि सम्भव नहीं, अतः कण, आरेख के किसी भी क्षेत्र में अस्तित्व में नहीं है।
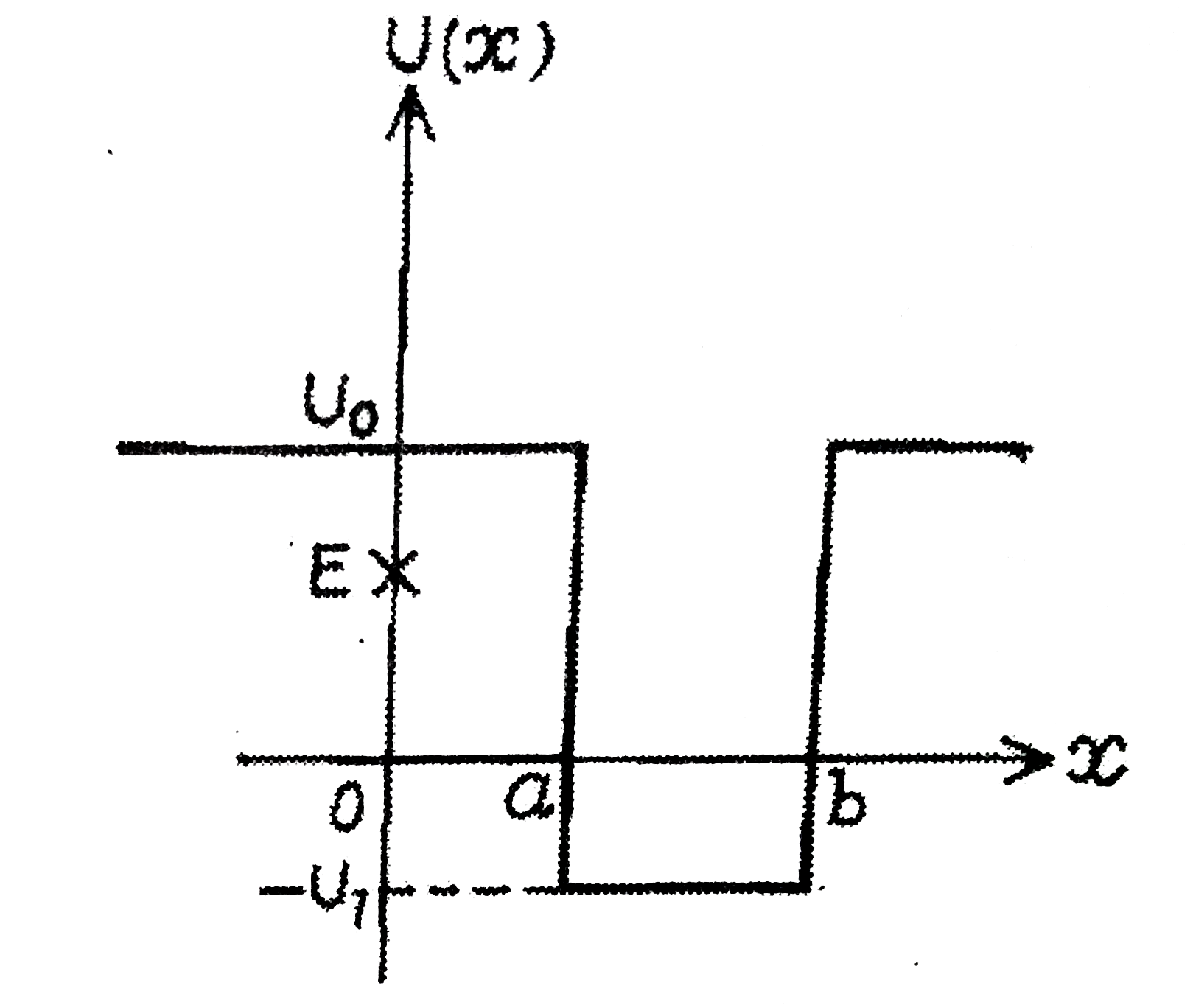
चित्र (c ) में क्षेत्र x lt a व x gt b कण की स्थितिज ऊर्जा `U=U_(0)` है, जो कि उसकी सम्पूर्ण ऊर्जा E से अधिक है अतः यह तथ्य गतिज ऊर्जा के ऋणात्मक मान की ओर संकेत करता है। अतः क्षेत्र x lt a व x gt b में कण अस्तित्व में नहीं हो सकता ।
परन्तु क्षेत्र x = a से x = b जिसमे कि न्यूनतम स्थितिज ऊर्जा `-U_(1)` है, में कण अस्तित्व में रह सकता है।
चित्र (d ) के क्षेत्र `a//2ltx lt b//2` तथा `-b//2lt xlt -a//2` में कण अस्तित्व में नहीं रह सकता ।