परस्पर दूरी पर स्थित m1 व m2 द्रव्यमानो के बीच गुरुत्वीय- बल Gm1m2/r2 होता है। स्थिरांक G का मान निर्भर करता है :
केवल मात्रको की पद्धति पर
केवल द्रव्यमानो के बीच माध्यम पर
दोनों पर
उपरोक्त में से किसी पर भी नहीं
The correct Answer is:A
Step by step video, text & image solution for परस्पर दूरी पर स्थित m_(1) व m_(2) द्रव्यमानो के बीच गुरुत्वीय- बल Gm_(1)m_(2)//r^(2) होता है। स्थिरांक G का मान निर्भर करता है : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सार्वत्रिक गुरुत्वाकर्षण BOOK - NOOTAN HINDICHAPTER - सार्वत्रिक गुरुत्वाकर्षण EXERCISE - अतिलघु उत्तरीय
24 Videos
- सार्वत्रिक गुरुत्वाकर्षण BOOK - NOOTAN HINDICHAPTER - सार्वत्रिक गुरुत्वाकर्षण EXERCISE - लघु उत्तरीय
28 Videos
- सार्वत्रिक गुरुत्वाकर्षण BOOK - NOOTAN HINDICHAPTER - सार्वत्रिक गुरुत्वाकर्षण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए
15 Videos
- सरल आवर्त गति BOOK - NOOTAN HINDICHAPTER - सरल आवर्त गति EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
34 Videos
Similar Questions
केप्लर का ग्रहो की गति सम्बन्धी द्वितीय नियम लिखिए।
View Solutionग्रहो की गति सम्बन्धी केप्लर के नियमो का उल्लेख कीजिए।
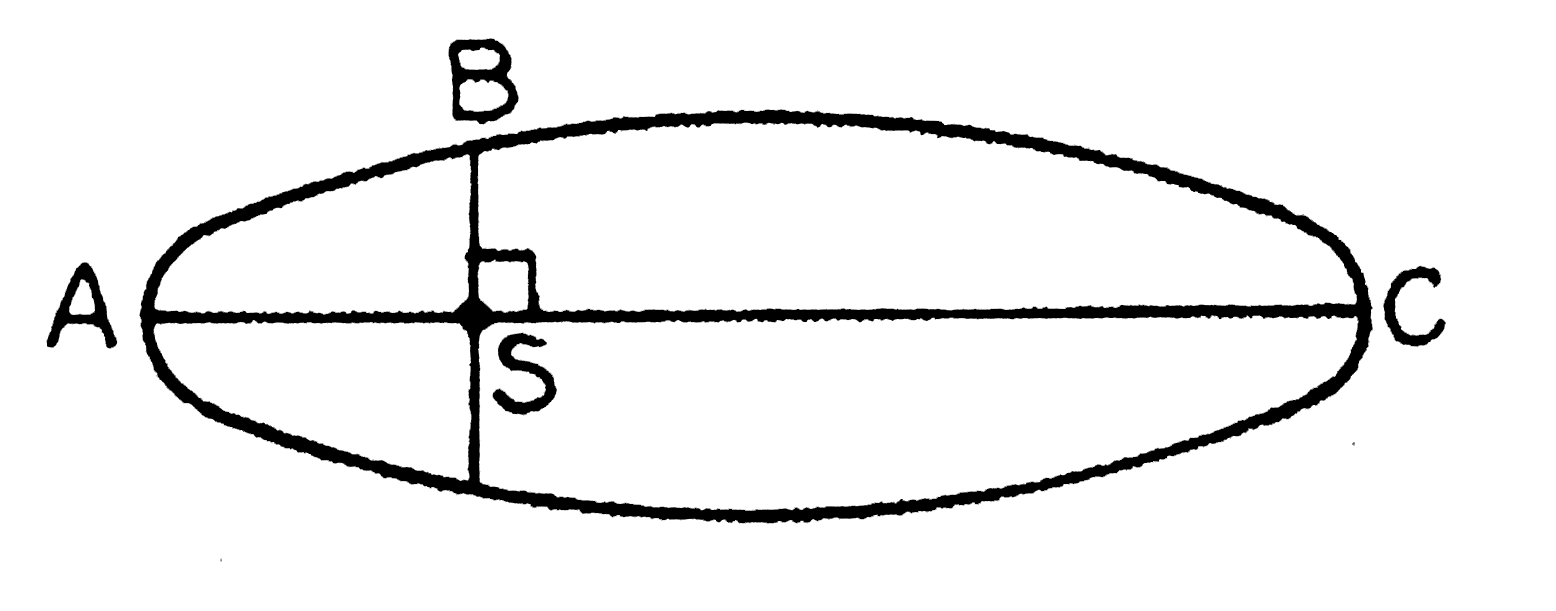
View Solutionसूर्य के चारो ओर दीर्घवृत्तीय कक्षा में गतिमान ग्रह की स्थितियों A, B तथा C पर गतिज ऊर्जाएं क्रमश: KA,KB और KCहै। AC दीर्घ अक्ष है तथा सूर्य की स्थिति S पर SB चित्रानुसार दीर्घ अक्ष AC पर लम्ब है। तब :
View Solutionएक कण का विस्थापन x=0.2(cos2πt2−sin2πt2) मीटर है कण की गति -
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View SolutionGravitational force, F=Gm1m2/r.
View Solutionसूत्र (m1x2+m2x1m1+m2,m1y2+m2y1m1+m2) क्या कहलाता है ?
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View Solutionनिम्न कथन सत्य या असत्य है-
सह -सम्बन्ध गुणांक का मान -2 से +2 के बीच होता है।
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
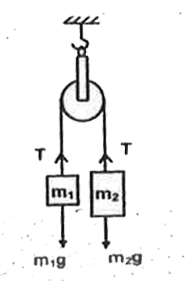
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View Solutionm1 व m2 द्रव्यमानों के दो कणों के किसी निकाय का द्रव्यमान केन्द्र, m1 से d1 दूरी पर तथा m2 से d2 दूरी पर इस प्रकार से है कि
View SolutionThe distance between two particles of masses m1andm2 is r. If the distance of these particles from the centre of mass of the system are r1andr2 respectively, then show that r1=r(m2m1+m2)andr2=r(m1m1+m2)
View SolutionF = (Gm_(1)m_(2))/(r^(2)) is valid
View Solution
