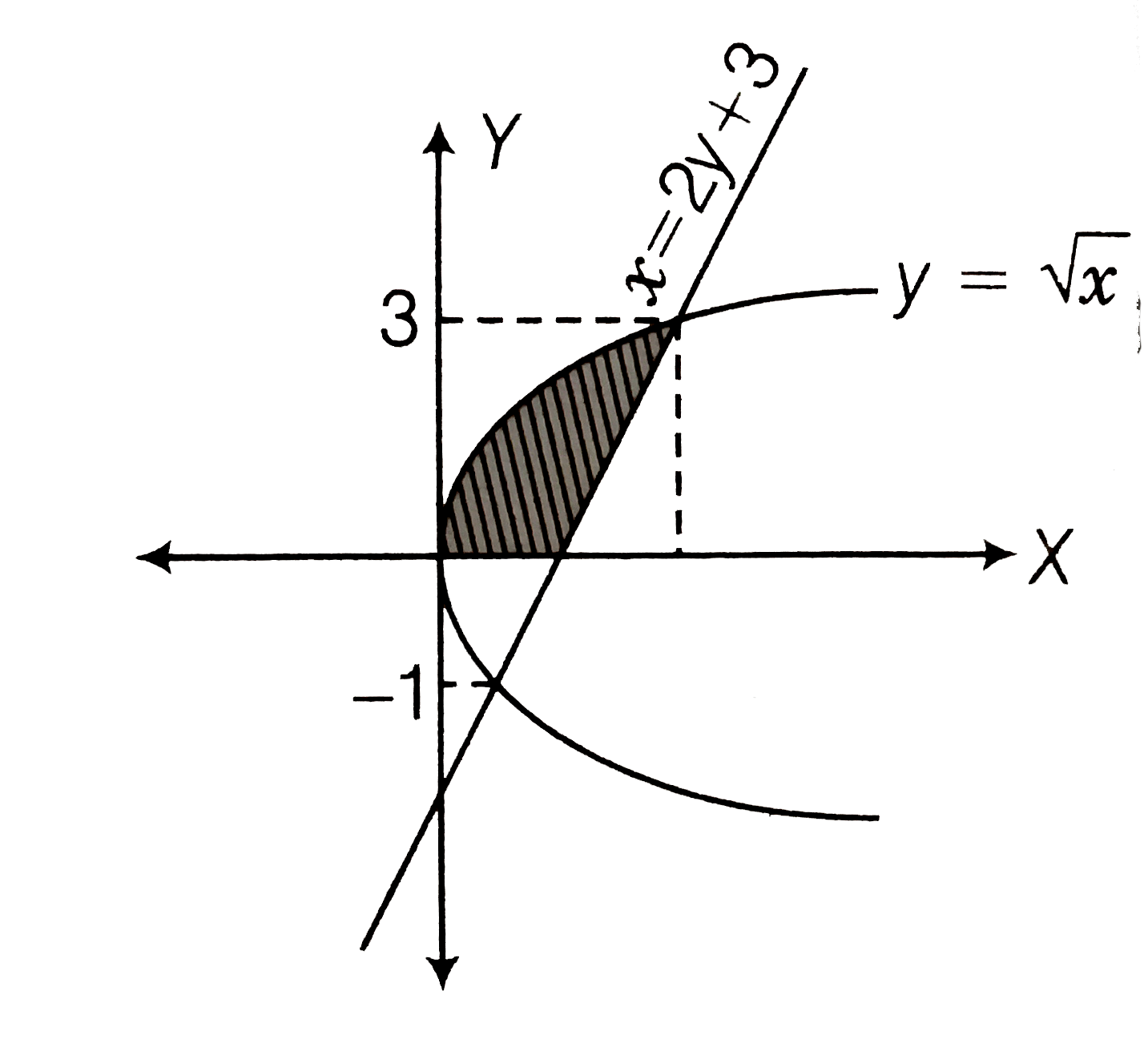
Find the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
Video Solution
Text Solution
The correct Answer is:N/a
Given equation of the curves are y=√x and x=2y+3 in the first quadrat.
On solving both the equations for y, we get
y=√2y+3
⇒y2=2y+3
⇒y2−2y−−3=0
⇒y2−3y+y−3=0
⇒y(y−3)+1(y−3)=0
⇒(y−1)(y−3)=0
⇒y=−1,3
∴ Required area of shaded region,
A=∫30(2y+3−y2)dy=[2y22+3y−y33]30
=[182+9−9−0]=9 sq units
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
A2√3B18C9D34/3
Find the area bounded by the curve y=4x2,x=0,x=1 and y=4 in first quadrant.
View SolutionFind the area bounded by the curve y=x3−3x2+2x and the x-axis.
View SolutionFind the area bounded by the curve y=x2,x=1,x=2 and x-axis .
View SolutionIf the area bounded by the curves y=√x,2y+3=x and the x-axis in the first quadrant is m2, then the value of m is equal to
View SolutionFind the area bounded by the curve y=−3|x|+2 and x-axis
View SolutionFind the area bounded by the curves y=x and y=x3
View SolutionFind the area bounded by the curve y2=36x, the line x = 2 in first quadrant .
View Solution
