ABCD is a rhombus whose one angle is 60∘.prove that the ratio of length of its diagonal is √3:1
Step by step video solution for ABCD is a rhombus whose one angle is 60^@.prove that the ratio of length of its diagonal is sqrt3:1 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023समान प्रश्न
ज्ञान जांच
Assertion (A) : If ABCD is a rhombus whose one angle is 60∘ then the ratio of the lengths of its diagonals is √3:1
Reason (R ) : Median of a triangle divides it into two triangle of equal area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.ABCD is a rhombus whose side AB=4cmand ∠ABC=120∘, then the length of diagonal BD is equal to :
A1 cmB2 cmC3 cmD4 cmIn a rhombus one side is 24 cm and one angle is 60°, then find the length of larger diagonal.
A12 cmB24√3cmC12sqsrtcmD6√3cm
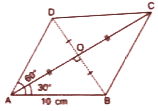
In a rhombus ABCD, length of each side is 10 cm and ∠A=60∘. Find the lengths of its diagonals AC and BD.
View SolutionThe acute angle of a rhombus whose side is a mean proportional between its diagonals is
View SolutionABCD is a rhombus with side 6 cm. If one of the diagonals is of 3√3 cm then length of other diagonal is
View SolutionArea of a rhombus is 144cm2 and the ratio of length of two diagonals is 1:2. The sum of lengths of its diagonals are :
View SolutionArea of a rhombus is 144cm2 and the ratio of length of two diagonals is 1:2. The sum of lengths of its diagonals are :
View Solution
