A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then 
(R2+R+1)(2–R)=1
(R2–R–1)(2–R)=1
(R2–R+1)(2–R)=1
(R2+R–1)(2–R)=1
The correct Answer is:A
NA
Topper's Solved these Questions
Similar Questions
A uniform sphere of radius R has a spherical cavity of radius R2 (see figure). Mass of the sphere with cavity is M. The sphere is rolling without sliding on a rough horizontal floor [the line joining the centre of sphere to the centre of the cavity remains in vertical plane]. When the centre of the cavity is at lowest position, the centre of the sphere has horizontal velocity V. Find:
(a) The kinetic energy of the sphere at this moment.
(b) The velocity of the centre of mass at this moment.
(c) The maximum permissible value of V ( in the position shown ) which allows the sphere to roll without bouncing
View SolutionA uniformly charged hemisphere of radius b and charge density ρ has a hemispherical cavity of radius a(a=b2) cut from its centre. If the potential at the centre of the cavity is nρb216ε0 then n=?
View Solution
Knowledge Check
- Question 1 - Select One
A solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
A+Q,−QB−Q,+QCQ,−QD+Q,0 - Question 2 - Select One
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
A1.5RB√3RC3RD2√3R - Question 3 - Select One
A metallic sphere of diameter D has a cavity of diameter d at its centre. If the sphere is heated, the diameter of the cavity will:
ADecreaseBIncreaseCRemain unchangedDDecrease if d<D/2 and increase if d>D/2
A solid spherical conductor of radius R has a spherical cavity of radius a(a+Q is kept at the center.The charge at the inner surface outer and at a position r(a<r<R)are respectively.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
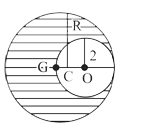View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View Solution