Find the first negative termof the sequence 2000, 1995, 1990, 1985,……
To find the first negative term of the sequence 2000, 1995, 1990, 1985, ..., we can follow these steps:
Step 1: Identify the first term and common difference
The first term a of the sequence is 2000. The common difference d can be calculated as follows:
d=1995−2000=−5
Step 2: Write the formula for the n-th term of the sequence
The n-th term an of an arithmetic progression (A.P.) can be expressed as:
an=a+(n−1)⋅d
Substituting the values of a and d:
an=2000+(n−1)(−5)
Step 3: Set up the inequality for the first negative term
We want to find the smallest n such that an<0:
2000+(n−1)(−5)<0
Step 4: Simplify the inequality
Rearranging the inequality gives:
2000−5(n−1)<0
2000−5n+5<0
2005−5n<0
5n>2005
n>20055
n>401
Step 5: Find the smallest integer n
Since n must be an integer, the smallest integer satisfying this inequality is:
n=402
Step 6: Calculate the 402nd term to verify
Now, we calculate a402:
a402=2000+(402−1)(−5)
=2000+401⋅(−5)
=2000−2005
=−5
Conclusion
The first negative term of the sequence is −5.
---
The first term a of the sequence is 2000. The common difference d can be calculated as follows:
d=1995−2000=−5
The n-th term an of an arithmetic progression (A.P.) can be expressed as:
an=a+(n−1)⋅d
Substituting the values of a and d:
an=2000+(n−1)(−5)
We want to find the smallest n such that an<0:
2000+(n−1)(−5)<0
Rearranging the inequality gives:
2000−5(n−1)<0
2000−5n+5<0
2005−5n<0
5n>2005
n>20055
n>401
Since n must be an integer, the smallest integer satisfying this inequality is:
n=402
Now, we calculate a402:
a402=2000+(402−1)(−5)
=2000+401⋅(−5)
=2000−2005
=−5
The first negative term of the sequence is −5.
Similar Questions
Knowledge Check
Find product in reaction sequence
 A
A B
B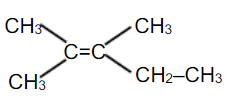 C
C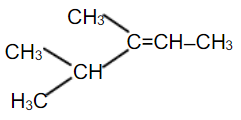 D
D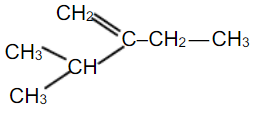
Find the sum of first 20 terms of the sequence 15×6+16×7+17×8+.....
A0.16B1.6C16D0.016
Write the first negative term of the sequence 20,1914,1812,1734…..
View SolutionFind the first negative term of the below A.P. 129, 120, 111,102, ......
View SolutionWhich term of the sequence 2005,2000,1995,1990,1985,……. Is the first negative term
View SolutionFirst negative term of series 998,996,994.....
View SolutionFind the first five terms of the sequence whose general term is given by
an=(−1)n3+n
View SolutionFind the first six terms of the sequence whose first temr is 1 and whose (n+1) th term is obtained by adding n to the nth term.
View Solution
