Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
Step by step video & image solution for Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Six X 's have to be placed in the squares of the figure below, such that each row contains atleast one X. in how many different ways can this be done?

View SolutionSix Ps have to be placed in the squares of the diagram given below such that each column contains at least one P. In how many ways this can be done?

View Solution
Knowledge Check
Six X ' s have to be placed in thesquares of the figure below, such that each rowcontains atleast one X. In how many different wayscan this be done?
A27B28C26D35
Six X's are to be placed in boxes of the figure such that each row contains at least one X, In how many different ways can this be done?A28B27C26D29Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
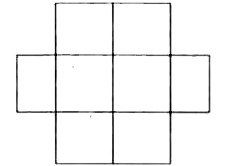 A25B26C27D30
A25B26C27D30
Six X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
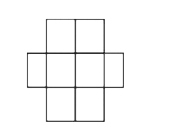
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:

View SolutionIn how many ways can 7 cross marks X be placed in the given figure so that each row has at least one cross mark?
View SolutionEach of 8 identical balls is to be placed in the squares shown in the figure given in a horizontal direction such that one horizontal row contains 6 balls and the other horizontal row contains 2 balls. In how many maximum different ways can this be done
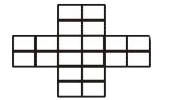
View SolutionThere are three different rings to be worn in four fingers with at most one in each finger. In how many ways can this be done?
View Solution
