Two sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is / are ('O' being the origin)
(1+√3,1+√3)
(−1−√3,−1−√3)
(3+√3,3+√3)
(√3−1,√3−1)
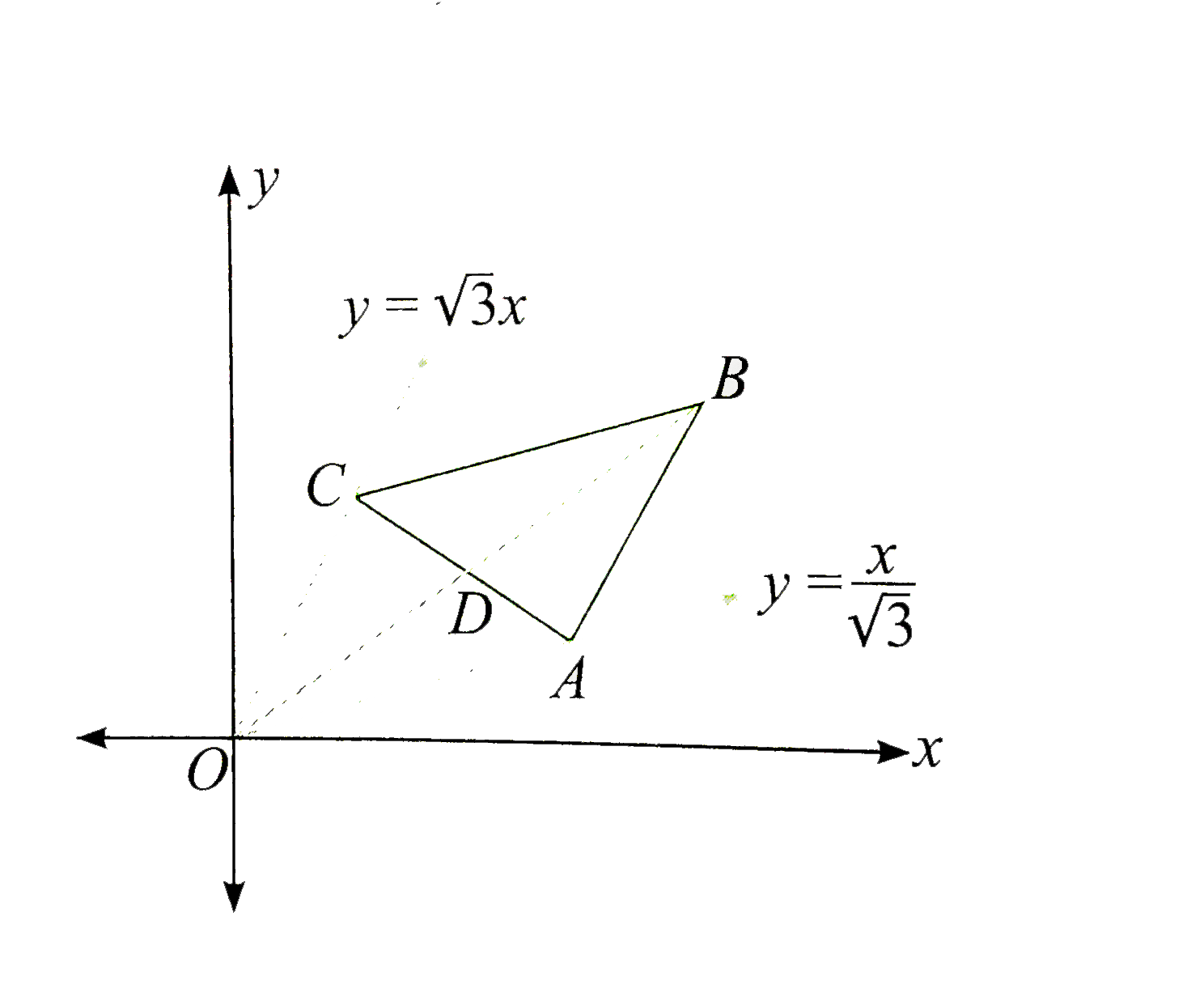
Here,∠COA=30∘.
Area of rhombus =2×12×OA×OCsin30∘
or 2=12x2
or OA = OC =2
Also, ∠OAB=150∘
∴ cos150∘=OA2+AB2−OB22OA×AB
OB2=8+4√3 or OB=√2(√3+1)
Hence, the coordinates of B are (±√2(√3+1) cos 45∘,±√2(√3+1)sin45∘).
Similar Questions
Two sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is / are ('O' being the origin)
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x-axis, and lying in the first quadrant is
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and Y- axis
View SolutionTwo sides of a rhombus OABC (lying entirely in the first of third quadrant ) of ara equal to 2 sq. units are y=x/√3,y=√3x. The the possible coordinates of B is/are (O being the origin)
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 the line x=√3y and x-axis , is
View SolutionThe area (in sq. units) of the region in the first quadrant bounded by y=x2,y=2x+3 and the y - axis is
View SolutionTwo sides of a rhombus OABC ( lying entirely in first quadrant or fourth quadrant) of area equal to 2 sq. units, are y=x√3,y=√3x Then possible coordinates of B is / are ('O' being the origin)
View SolutionThe area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x-axis, and lying in the first quadrant is
View Solution
