दी आकृति में, ABC एक त्रिभुज है तथा भुजा BC पर एक बिन्दु P इस प्रकार है की AB = AP है | यदि बढ़ाई गई AP, ΔABC के परिवृत्त को Q पर मिलती है तो सिद्ध कीजिए कि CP = CQ.
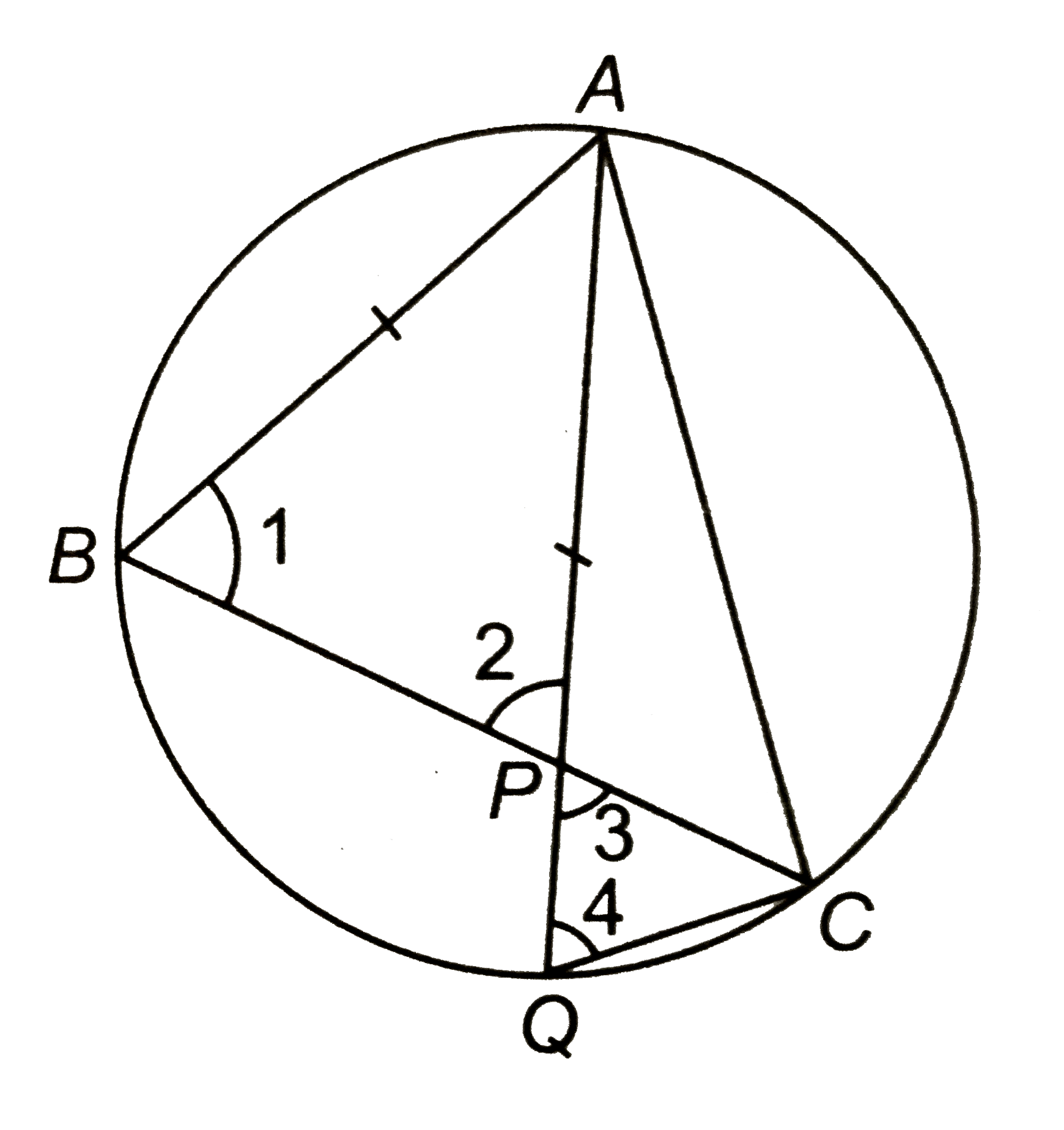
ΔABP, में
AB=AP (दियाहै)
∠1=∠2 (समान भुजाओं के सम्मुख कोण) …(1)
परन्तु ∠2=∠3 (शीर्षाभिमुख कोण) ...(2)
⇒ ∠1=∠3 [समीकरण (1) और (2) से] ...(3)
परन्तु ∠1=∠4 (एक वृत्तखण्ड के कोण) ...(4)
∴ ∠3=∠4 [समीकरण (3) और (4) से]
⇒ CP=CQ (ΔCPQ में समान कोणों कि सम्मुख भुजाएँ)
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10A
21 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10B
19 Videos
- रेखाएं और कोण BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन
5 Videos
- संख्या पद्धतिBOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
10 Videos
Similar Questions
एक वृत्त में 10 सेमी लम्बी जीवा केन्द्र से 12 सेमी कि दूरी पर है | इसी वृत्त के केन्द्र से 5 सेमी की दूरी पर स्थित जीवा की लम्बाई क्या होगी ?
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि ∠ACB=25∘, तो ∠AOB ज्ञात कीजिए |

View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
View SolutionMatch the following Column A to Column B

View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
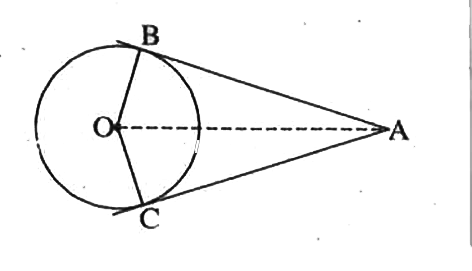
View Solutionदी गई आकृति AT वृत्त की स्पर्श रेखा है। यदि m∠ABC=50∘ तथा AC=BC तो ∠BAT है -

View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
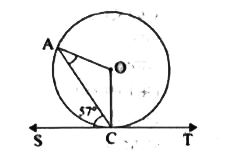
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solution
