Let a complex number α,α11≠1 be a root of the equation z18−z7−z11+1=0, then identify the correct option :
Step by step video solution for Let a complex number alpha, alpha^11 != 1 be a root of the equation z^18 - z^7 - z^11 + 1 = 0, then identify the correct option : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
For a complex number Z, if one root of the equation Z2−aZ+a=0 is (1+i) and its other root is α, then the value of aα4 is equal to
A4B−14C2D−2Let α and β be real number and z be a complex number. If z2+αz+β=0 has two distinct non-real roots with Re(z) =1, then it is necessary that
Aβ∈(−1,0)B|β|=1Cβ∈(1,∞)Dβ∈(0,1)If 2 = 1 + ai is a complex number, a>0, such that z3 is a real number. Then the value of the sum 1+z+z2+……+z11 is equal to,
A1365√3iB−1365√3iC−1250√3iD1250√3i
For a complex number Z, if one root of the equation Z2−aZ+a=0 is (1+i) and its other root is α, then the value of aα4 is equal to
View SolutionLet z=1+ai be a complex number, a>0,such that z3 is a real number. Then the sum 1+z+z2+...+z11 is equal to:
View SolutionLet z1,α,β be complex numbers of which αandβ constants and z1 varies. If z2 is given in terms of z1 by one of the following equations, it is required to find z2 corresponding to z1 then
In the given figure
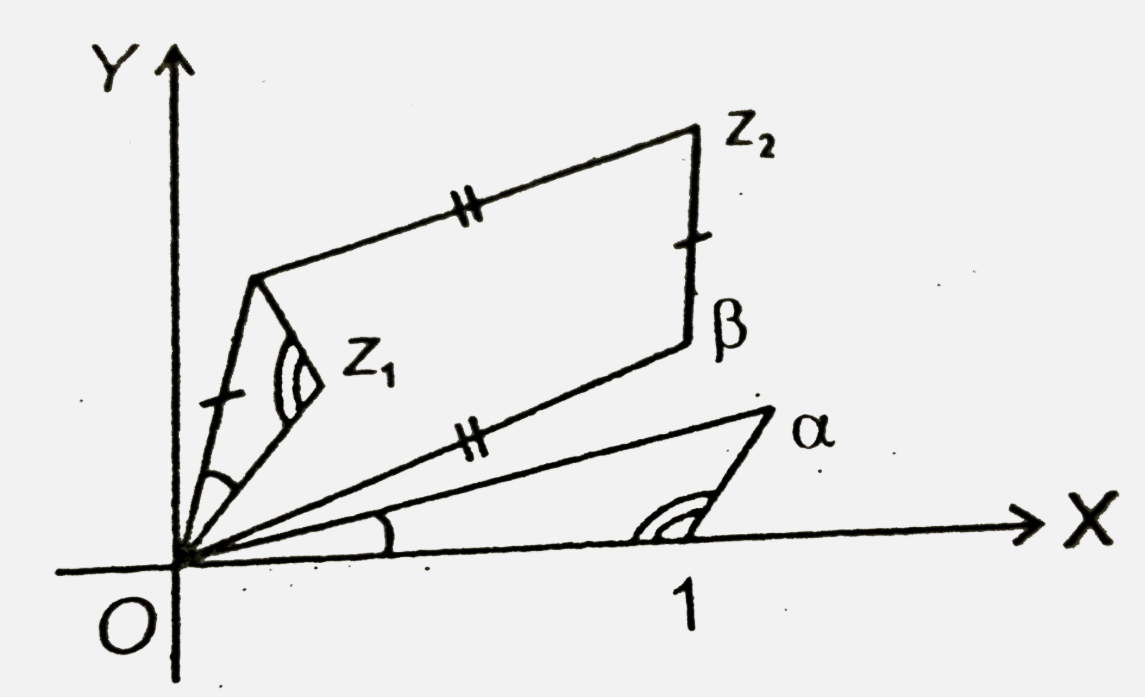
View SolutionLet z1,α,β be complex numbers of which αandβ constants and z1 varies. If z2 is given in terms of z1 by one of the following equations, it is required to find z2 corresponding to z1 then The given figure illustrates
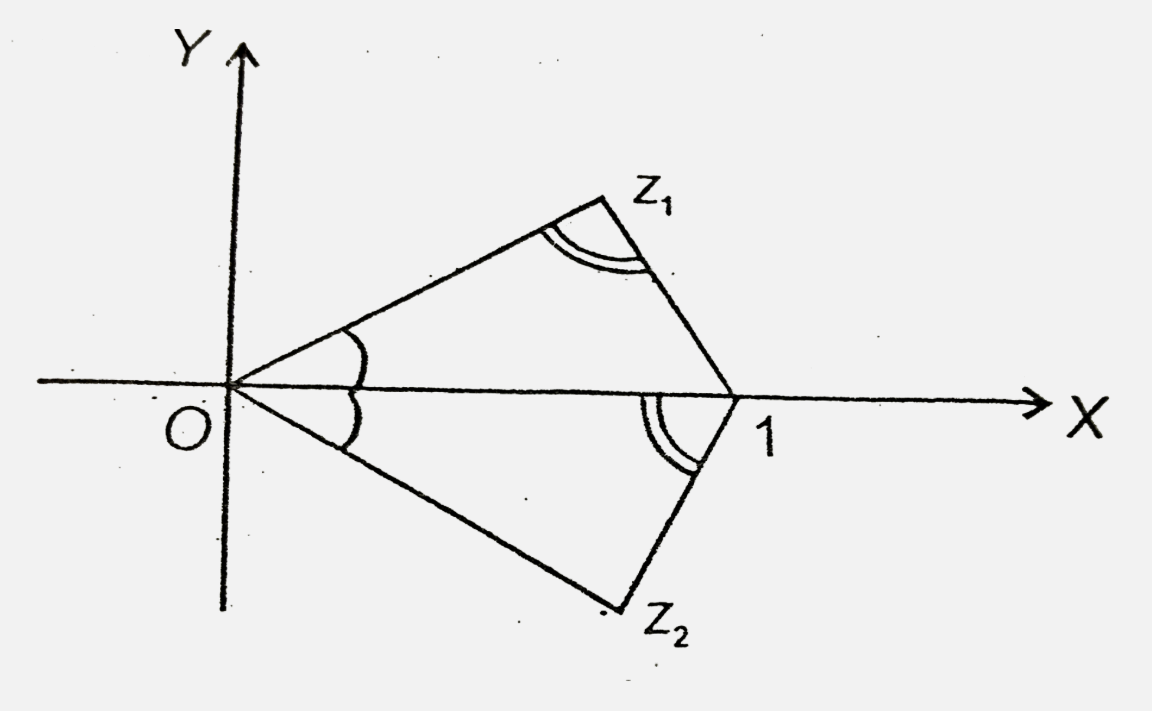
View SolutionIf the imaginary part of the complex number (z−1)(cosα−isinα)+(z−1)−1(cosα+isinα) is zero, then which of the following options are correct? a) |z|=1 b) |z−1|=1 c) arg(z)=α d) arg(z−1)=α
View Solution
