Two tangents PA and PB are drawn to a circle with centreO fr om an external point P. Prove that ∠APB=2∠AOB
Step by step video solution for Two tangents PA and PB are drawn to a circle with centreO fr om an external point P. Prove that /_APB=2/_AOB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
From an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
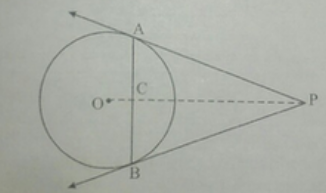
View SolutionThe center of the circle in the picture is O. The tangent lines PA and PB are drawn from the external point P if /_ACB=50^(@) , so /_APB Will measure
View SolutionO केंद्र वाले वृत्त पर बाह्य बिंदु P से क्रमश: PA और PB स्पर्श रेखाएं खींची गई हैं। M बिंदु से खींची गई स्पर्श रेखा PA और PB को K तथा N बिंदु पर काटती है, तो सिद्ध कीजिए- KN=AK+BN
View SolutionPA and PB are two tangents drawn from an external point P at the points A and B on a circle C(0,r).Prove that OP⊥AB
View SolutionTwo tangents PA and PB are drawn to circle with centre O from an external point P. Prove that ∠APB=2∠OAB
View Solutionएक वृत्त C(O, r) के बाह्य बिंदु P से वृत्त पर PA और PB दो स्पर्श रेखाएँ इस प्रकार खींची गई हैं कि ∠APB=120∘है। सिद्ध करो कि OP=2AP
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View SolutionThe tangents at two points A and B on the circle with centre O Intersects at P, If in quadrilateral AOBP,∠AOB:∠APB=5:1, then measure of ∠APBis:
View Solution
