PA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
a rectange
a rhombus
a square
cyclic quadrilateral
To determine the nature of the quadrilateral OAPB formed by the tangents PA and PB from an external point P to a circle centered at O, we can follow these steps:
1. Identify the Elements:
- Let O be the center of the circle.
- Let A and B be the points where the tangents PA and PB touch the circle.
- Let P be the external point from which the tangents are drawn.
2. Understand the Properties of Tangents:
- The lengths of the tangents drawn from an external point to a circle are equal. Thus, PA = PB.
- The radius of the circle (OA and OB) is perpendicular to the tangent at the point of contact. Therefore, angle OAP = 90° and angle OBP = 90°.
3. Label the Angles:
- Let angle APB be denoted as θ.
- Since OAP and OBP are both right angles, we have:
- angle OAP = 90°
- angle OBP = 90°
4. Sum of Angles in Quadrilateral OAPB:
- The sum of the angles in any quadrilateral is 360°. Therefore, we can write:
angle OAP+angle APB+angle PBO+angle OAB=360°
- Substituting the known angles:
90°+θ+90°+angle OAB=360°
- Simplifying this gives:
180°+θ+angle OAB=360°
- Thus, we find:
angle OAB=180°−θ
5. Check the Opposite Angles:
- We see that:
- angle OAP + angle OAB = 90° + (180° - θ) = 270° - θ
- angle APB + angle PBO = θ + 90° = θ + 90°
- The sum of opposite angles is:
angle OAP+angle PBO=90°+90°=180°
angle APB+angle OAB=θ+(180°−θ)=180°
6. Conclusion:
- Since the sum of the opposite angles in quadrilateral OAPB is 180°, it satisfies the condition for being a cyclic quadrilateral.
Final Answer:
The quadrilateral OAPB is a cyclic quadrilateral.
- Let O be the center of the circle.
- Let A and B be the points where the tangents PA and PB touch the circle.
- Let P be the external point from which the tangents are drawn.
- The lengths of the tangents drawn from an external point to a circle are equal. Thus, PA = PB.
- The radius of the circle (OA and OB) is perpendicular to the tangent at the point of contact. Therefore, angle OAP = 90° and angle OBP = 90°.
- Let angle APB be denoted as θ.
- Since OAP and OBP are both right angles, we have:
- angle OAP = 90°
- angle OBP = 90°
- The sum of the angles in any quadrilateral is 360°. Therefore, we can write:
angle OAP+angle APB+angle PBO+angle OAB=360°
- Substituting the known angles:
90°+θ+90°+angle OAB=360°
- Simplifying this gives:
180°+θ+angle OAB=360°
- Thus, we find:
angle OAB=180°−θ
- We see that:
- angle OAP + angle OAB = 90° + (180° - θ) = 270° - θ
- angle APB + angle PBO = θ + 90° = θ + 90°
- The sum of opposite angles is:
angle OAP+angle PBO=90°+90°=180°
angle APB+angle OAB=θ+(180°−θ)=180°
- Since the sum of the opposite angles in quadrilateral OAPB is 180°, it satisfies the condition for being a cyclic quadrilateral.
The quadrilateral OAPB is a cyclic quadrilateral.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two circles touch each other externally at a point P and a direct common tangent touches the circles at the points Q and R respectively. Then ∠QPR is
A45∘B180∘C90∘D60∘Choose the CORRECT option about the two tangents drawn to the circle from the external point?
1. The tangents subtend equal angles at the centre of the circle.
2. The tangents drawn from the external point to a circle are equal in length.
3. The tangents are equally inclined to the segment which joins the centre to that point.A1 and 2 onlyB2 and 3 onlyC1, 2 and 3D1 and 3 onlyPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘
Theorem: The length of two tangents drawn from an external point to a circle are equal.
View SolutionThe number of tangents drawn from an external point to a circle is _____________.
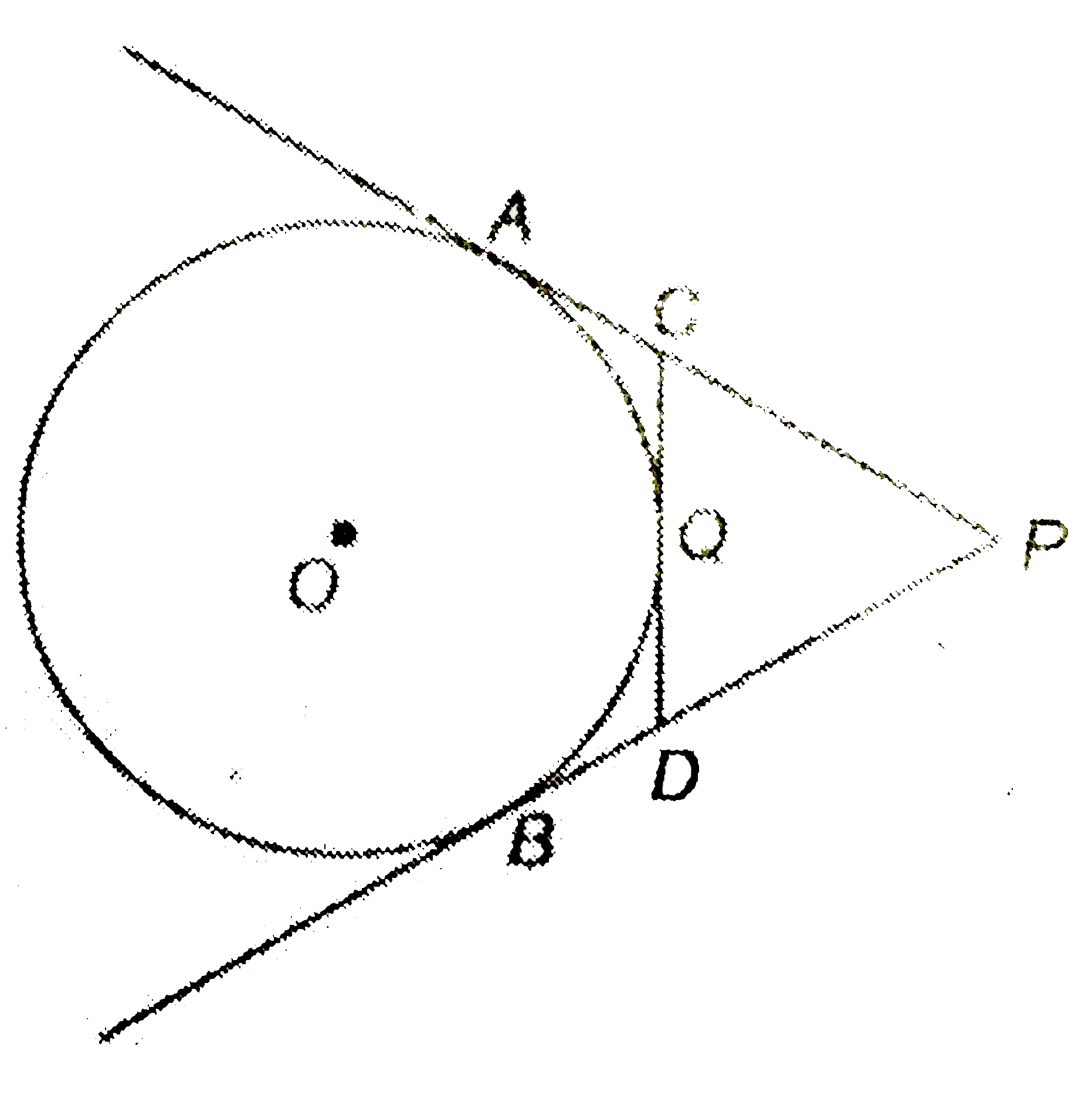
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
View Solution
The length of tangents drawn from the external point to a circle are ........... .
View SolutionO is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
View Solution
