Assume that the temperature remains essentially constant in the upper part of the atmosphere. Obrain an epression for the variation in pressure in the upper atmosphere with height, the mean molecular weight of air is M.
Suppose the pressure at height h is p and that at
Now considering any small volume if air of mass
Putting in (i),
ltbr>int_(p_(0))^(p)(dp)/(p)=int_(0)^(h)-(M)/(RT)g dhor, In(p)/(p_(0))=-(Mgh)/(RT)
Thus,
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Short Answer
14 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 1
17 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercises
62 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
(a) Assume the atmosphere as an ideal gas in static equilibrium at constant temperature T0. The pressure on the ground surface is P0. The molar mass of the atmosphere is M. Calculate the atmospheric pressure at height h above the ground.
(b) To be more realistic, let as assume that the temperature in the troposphere (lower part of the atmosphere) decreases with height as shown in the figure. Now calculate the atmospheric pressure at a height h0 above the ground.
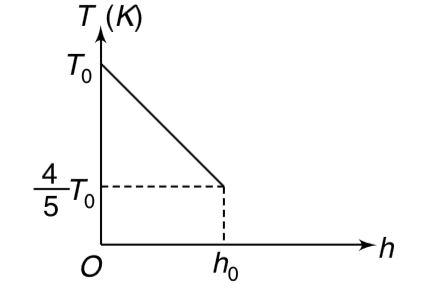
View SolutionShow that the internal energy of the air (treated as an ideal gas) contained in a room remains constant as the temperature changes between day and gight. Assume that the atmospheric pressure around remains constant and the air in the room maintains this prssure by communicating with the surrounding thourgh the widows, doors, etc.
View Solution
Knowledge Check
Assume that the temperature remains essentially constant in the upper parts of the atmosphere. The atmospheric pressure varies with height as. (the mean molecular weight of air is M, where P0= atmospheric pressure at ground reference)
APe−3Mgh2RTBP0e−Mgh2RTCP0e−3MghRTDP0eMghRTNormally, the temperature decreases with the increase in height from the Earth's surface, because -
1. the atmosphere can be heated upwards only from the Earth's surface
2. there is more moisture in the upper atmosphere
3. the air is less dense in the upper atmosphere
Select the correct answer using the codes given below:Al onlyB2 and 3 onlyC1 and 3 onlyD1, 2 and 3Normally, the temperature decreases with the increase in height from the Earth’s surface because
1. The atmosphere can be heated upwards only from the Earth’s surface.
2. There is more moisture in the upper atmosphere.
3. The air is less dense in the upper atmosphere.
Select the correct answer using the codes given below:A1 onlyB2 and 3 onlyC1 and 3 onlyD1, 2 and 3
Which of the following statements concerning atmosphere of the Earth are correct?
1. In statosphere, temperature increases with altitude.
2. In mesophere, temperature decreases with altitude.
3. The lowest temperature of the atmosphere is recorded inthe upper part of mesosphere.
4. Tropopause is an isothermal zone.
Select the correct answer using the code given below
View SolutionDiameter of a planet is 10d∘, its mean density is ρ∘4 and mass of its atmosphere is 10m∘ where d∘, ρ∘ and m∘ are diameter, mean density and mass of atmosphere respectively for the earth. Assume that mean density of atmosphere is same on the planet and the earth and height of atmosphere on both the planets is very small compared to their radius. Find the ratio of atmospheric pressure on the surface of the planet to that on the earth. If a mercury barometer reads 76 cm on the surface of the earth, find its reading on the surface of the planet.
View SolutionThere is a long vertical tube of radius r containing air at atmospheric pressure. A steel ball is held at the mouth of the tube and dropped. The ball has radius r and it just fits inside the tube. The tube wall is perfectly smooth and no air can leak from the tube as the ball falls inside it. The ball falls through half the length of the tube before coming to rest. Assume that wall of the tube is perfectly conducting and temperature of the air inside the tube remains constant. Density of steel is d and atmospheric pressure is P0 and take L>>r. Take air to be an ideal gas.
(a) Find the radius (r) of the tube.
(b) At what depth from the top of the tube the ball will be in equilibrium?
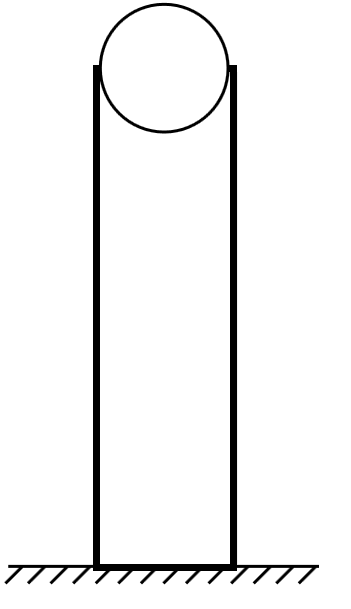
View SolutionThe temperature of a room of volume Vrise from T1 to T2. How much will the mass of the air in the room changes if the atmospheric pressure is p0. The molecular weight of the air is M.
View SolutionAn upper air wind system with very high velocities in certain parts of the atmosphere is called :
View Solution
