A horizontal tube of length I closed at both ends contains an ideal gas of molecular weight M, The tube is roatated at a constant angular velocity $ω$ about a vertical axis passing through an end. Assuming the temperature to be uniforme and constant, show that
$p_{2} = p_{1} e^{\frac{M ω^{2} l^{2}}{2 R T},}$
where p_(2) and p_(1)denote the pressures at the free end and the fixed end respetively.

Video Solution

Text Solution

Verified by Experts

Consider an element of the gas between the cross sections at distances x and $x + d x$ from the fixed end . If p be the pressure at x and $p + d p a t x + d x,$ the force acting in the element towards the centre is Adp, where A is the cross sectional area. As this element is going in a circle of radius X,
$A d p = (d m) (ω^{2}) x ... (i)$
where dm=mass of the element. Using $p V = n R T$ on this element,
$p A d x = \frac{d m}{M} R T$
$or, d m = \frac{M p A}{R T} d x .$
Putting in (i),
$A d p = \frac{M p A}{R T} (ω^{2}) x d x$
$or, \int_{p_{1}}^{p_{2}} \frac{d p}{p} = \int_{0}^{l} \frac{m (ω^{2})}{R T} x d x$
$I n \frac{p_{2}}{p_{1}} = \frac{M (ω^{2}) l^{2}}{2 R T}$
$(p_{2} = p_{1}) e^{\frac{M_{ω}^{2} l^{2}}{2 R T}}$ .

A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
For an L shaped conducting rod placed in an uniform magnetic field $\to B$ rotating with constant angular velocity $ω$ about an axis passing through one of its ends A and normal to the plane of the conductor induced emf

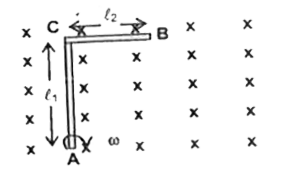Aacross AC equals $ω B l_{1}^{2}$
Bacross AC equals $\frac{1}{2} ω B l_{1}^{2}$
Cacross BC equals zero
DNone of the above is correct
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity $ω$ in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
A $\frac{m ω^{2} l^{2}}{6 A Y}$
B $\frac{m ω^{2} l^{2}}{3 A Y}$
C $\frac{m ω^{2} l^{2}}{A Y}$
D $\frac{m ω^{2} l^{2}}{2 A Y}$