A continuous function y=f(x) is defined in a close interval [-7,5]. A(-7,-4), B(-2,6), C(0,0), D(1,6), E(5,-6) are consecutive points on the graph of f and AB,BC,CD,DE are line segments. The number of real roots of the equation f(f(x)) = 6 is :
Step by step video solution for A continuous function y=f(x) is defined in a close interval [-7,5]. A(-7,-4), B(-2,6), C(0,0), D(1,6), E(5,-6) are consecutive points on the graph of f and AB,BC,CD,DE are line segments. The number of real roots of the equation f(f(x)) = 6 is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Suppose that the graph of y=f(x), contains the points (0,4)and(2,7). If f' is continuous then ∫20f'(x)dx is equal to
A2B−2C3Dnone of theseIf f is a linear function such that f(7)=5,f(12)=-6, and f(x)=23.7, what is the value of x?
A-3.2B-1.5C1D2.4
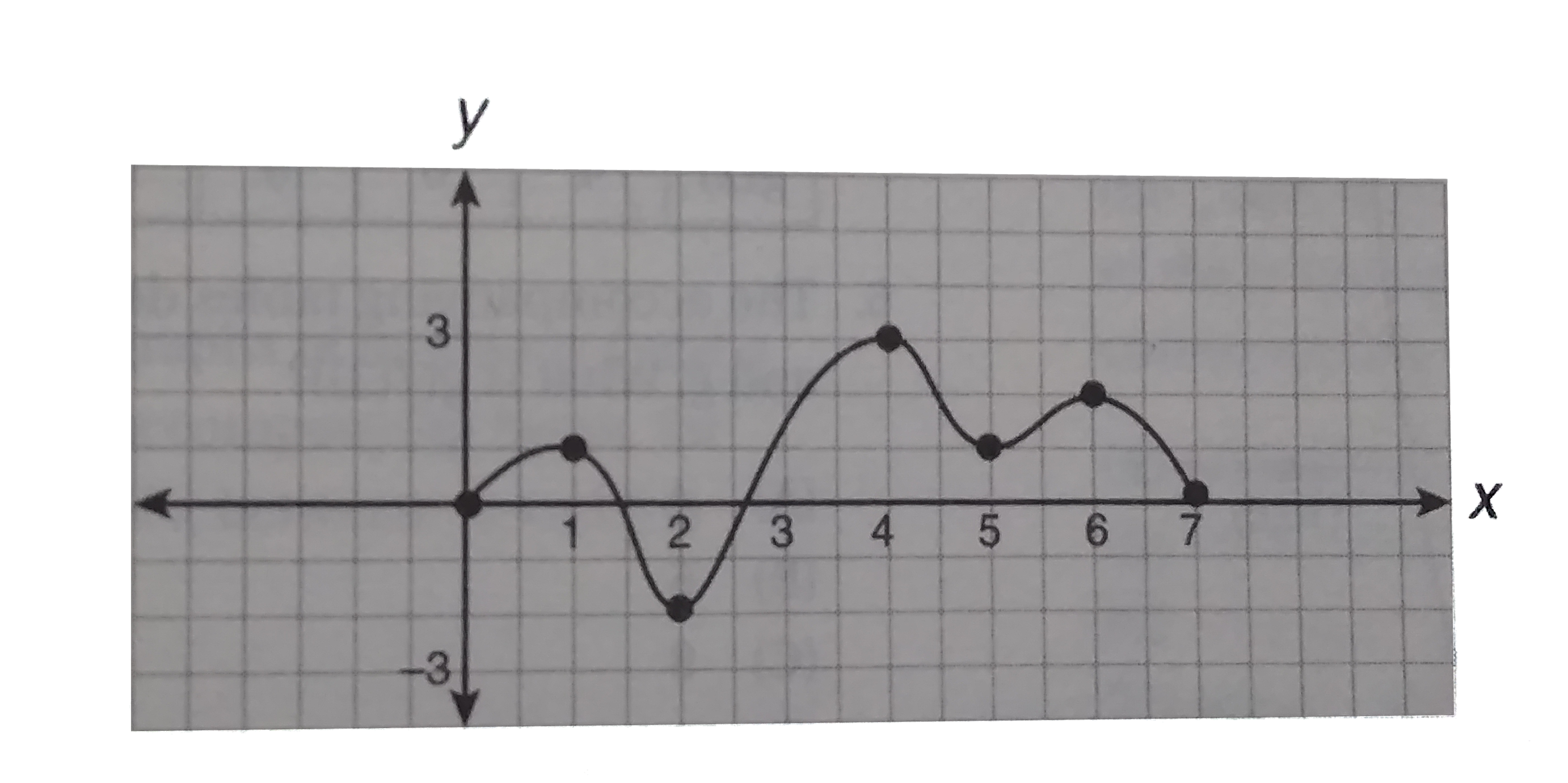
The graph above shows the function y=f(x) over the interval 0≤x≤7. What is the value of f(f(6))?
View SolutionThe maximum value of the function f(x)=(1+x)0.61+x0.6 in the interval [0,1] is 20.4 (b) 2−0.4 1 (d) 20.6
View SolutionIf f and g are two real functions defined by f={(a,1)(b,0),(c,8),(0,4)} and g={(a,5),(c,-3),(b,6)(0,2)} then dom (√gf) is
View SolutionIf f is an even function defined on the interval (−5,5), then four real values of x satisfying the equation f(x)=f(x+1x+2) are ______, __________, _______ and______.
View SolutionA function y−f(x) has a second-order derivative fx=6(x−1). It its graph passes through the point (2,1) and at that point tangent to the graph is y=3x−5, then the value of f(0) is 1 (b) −1 (c) 2 (d) 0
View SolutionA function y=f(x) has a second-order derivative f''(x)=6(x−1). It its graph passes through the point (2,1) and at that point tangent to the graph is y=3x−5, then the value of f(0) is 1 (b) −1 (c) 2 (d) 0
View Solution
