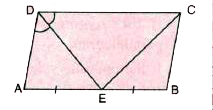
If ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
Step by step video solution for If ABCD is a parallelogram, E is the mid-point of AB and CE bisects /_BCD, then /_DEC is by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by ACIn the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
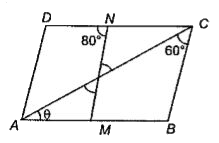 A20∘B30∘C40∘D10∘
A20∘B30∘C40∘D10∘In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
 A20*B30*C40*D10*
A20*B30*C40*D10*
ABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

∠DEC=90∘
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH

View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionIn the given figure, ABCD is a parallelogram, in which is the mid-point of ADandO is a point on AC such that AO=14AC. When EO produced, meets AB at F. Prove that F is the mid-point of AB.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Provethat:(i) AE=AD(i) DE bisects ∠ADC and(ili) Angle DEC is a right angle.
View Solution