दी गई आकृति में, एक वर्ग DEFG है तथा ∠BAC=90∘ है तो सिद्ध कीजिए कि
(i) △AFG~△DBG
(ii) △AGF~△EFC
(iii) △DBG~△EFC
(iv) (DE)2=BD×EC
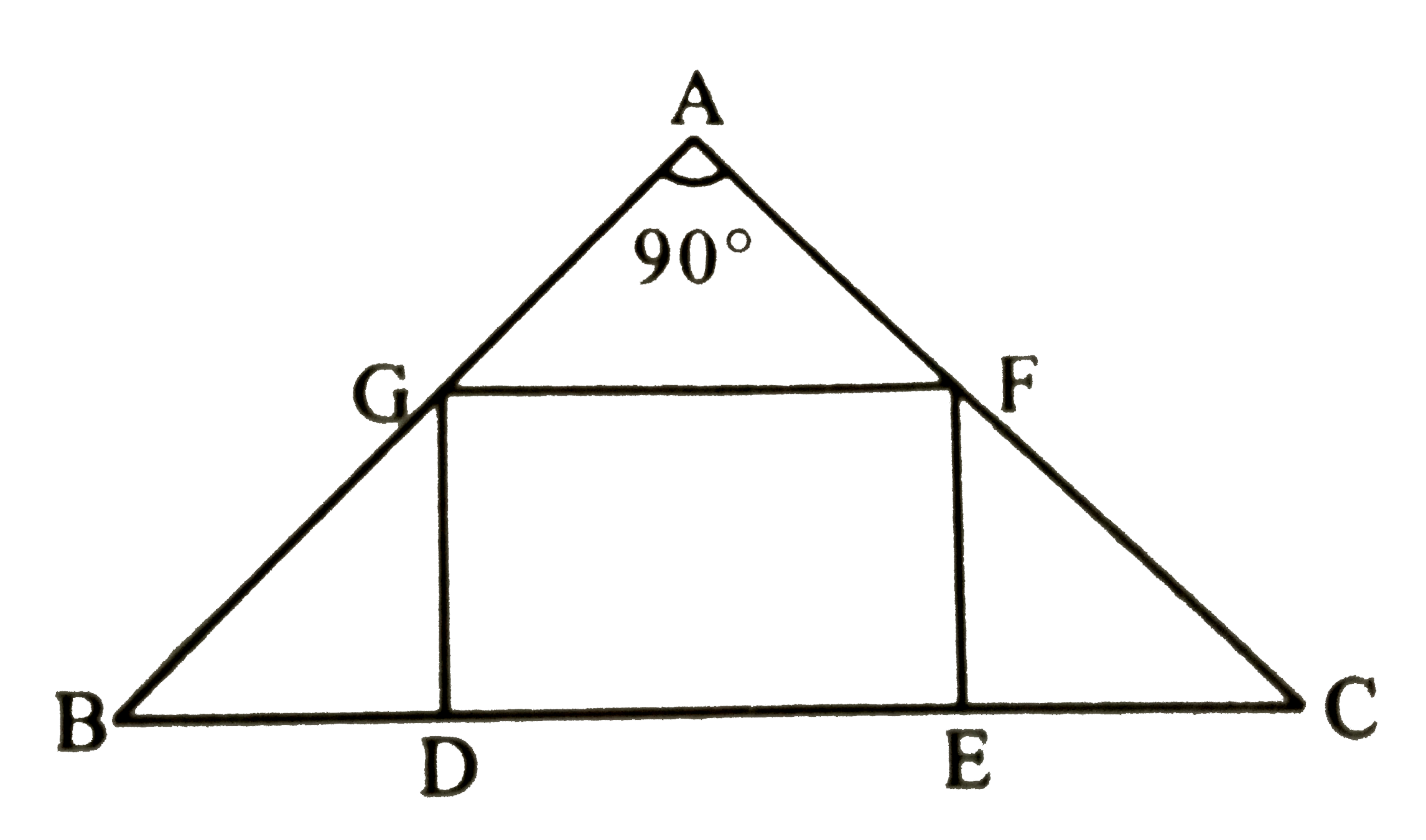
(i) △AGH तथा △DBG से,
∠GAF=∠BDG (प्रत्येक =90∘)
तथा ∠AGF=∠dBG (संगत कोण)
तब समरूपता की AA-कसौटी द्वारा,
△AGF~△DBG
(ii) अब △AGF तथा △EFC में, ∠FAG=∠CEF (प्रत्येक =90∘)
∠AFG=∠ECF (सगट कोण )
तब समरूपता की AA-कसौटी द्वारा,
△AGF~△EFC
(iii) चूँकि △AGF~△DBG तथा △AGF~△EFC
इसलिए, △DBG~△EFC
(iv) निष्कर्ष (iii) से, △DBG~△EFC
तब आधारभूत समानुपातिक प्रमेय द्वारा,
BDEF=DGEC
चूँकि DEFG एक वर्ग है, EF=DE,DG=DE
इसलिए, BDDE=DEEC⇒(DE)2=BD×EC
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
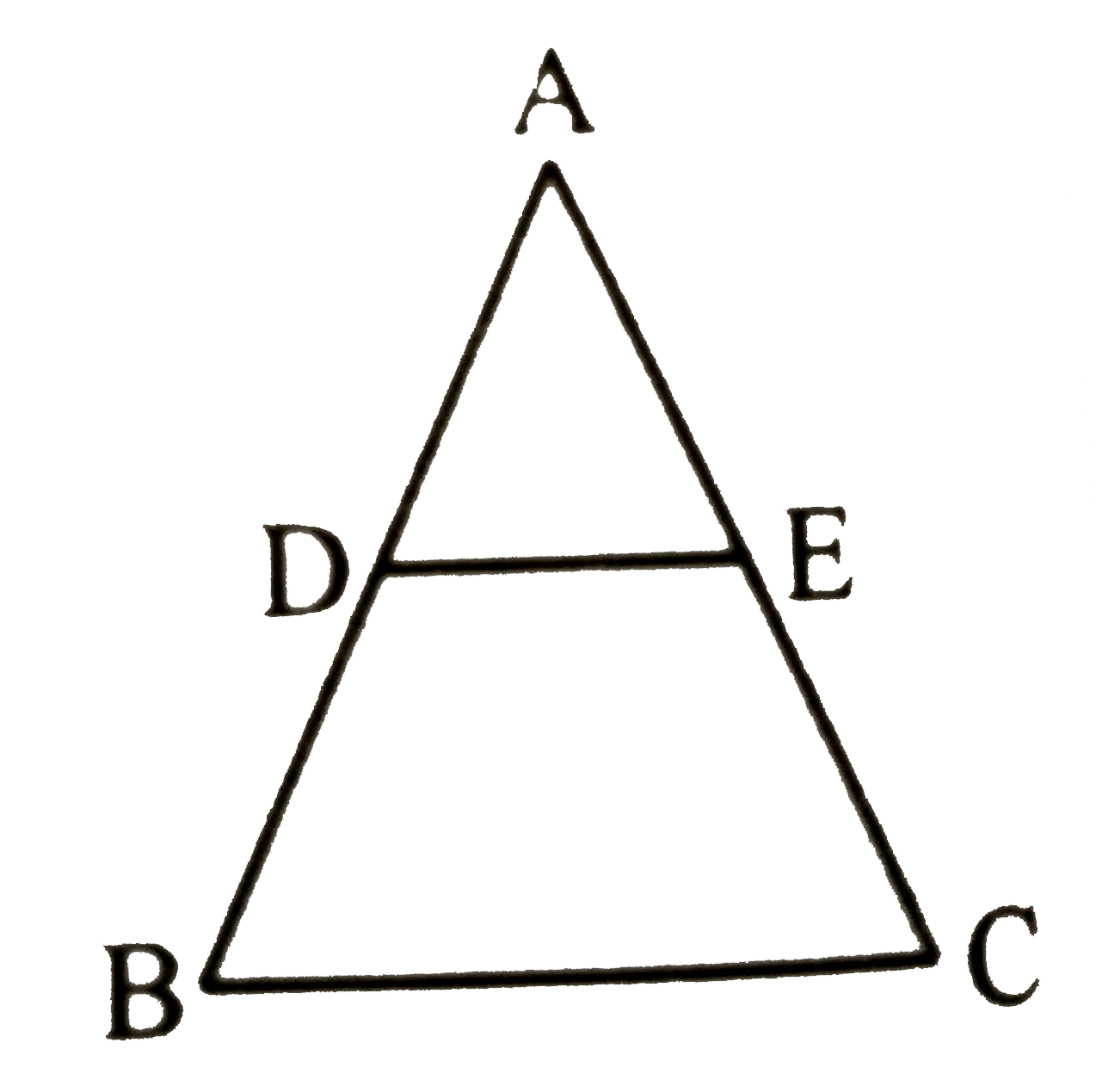
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionIn the following figure (not to scale), ABC is a right isosceles triangle, right- angle at B and BD⊥AC. If the triangle ABC is rotated about the hypotenuse, then find the locus of the triangle ABC. ltbr gt ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E02_006_Q01.png" width="80%"gt
View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View Solution
