In the given figure, DEFG is a square and ∠BAC=90∘, Prove that
(i)ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii)DE2=BD×EC

GIVEN AΔABC in which ∠ABC=90∘andDEFG is a squre.
TO PROOVE (i) ΔAGF~ΔDBG(ii)ΔAGF~ΔEFC
(iii)ΔDBG~ΔEFC(iv)DE2=BD×EC.
PROOF (i) In ΔAGFandΔDBG, we have
∠GAF=∠BDG=90∘
∠AGF=∠DBG [ orresponding ∠]
[ ∴GF∣∣BCandAB is the tranveral]
∴ΔAGF~ΔDBG.
(ii) In ΔAGFandΔEFC, we have
∠FAG=∠CEF=90∘
∠GFA=an≥lFCE [ correpsonidng ∠]
[ ∴GF∣|BC|andAC is the transverasal]
∴ΔAGR~ΔEFC.
(iii) ΔDBG~ΔAGFandΔAGF~ΔEFC
⇒ΔDBG~ΔEFC.
(iv) ΔDBG~ΔEFC⇒BDFE=DGEC
⇒BDDE=DEEC[∴DEandFE=DE]
Hence, DE2=BD×EC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
In the figure, DEFG is a square and ∠BAC=90∘. Prove that
(A) ΔAGF~ ΔDBG
(B)ΔAGF~ΔEFC
(C) ΔDBG~ΔEFC
 View Solution
View SolutionIn the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
View SolutionIn the given figure, ∠1=∠2andACBD=CBCE prove that ΔACB~ΔDCE.
 View Solution
View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.
 View Solution
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.
 View Solution
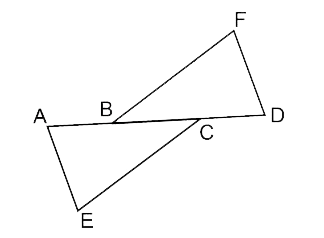
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE=∠DBF . Prove that
△ACE≅△DBF
 View Solution
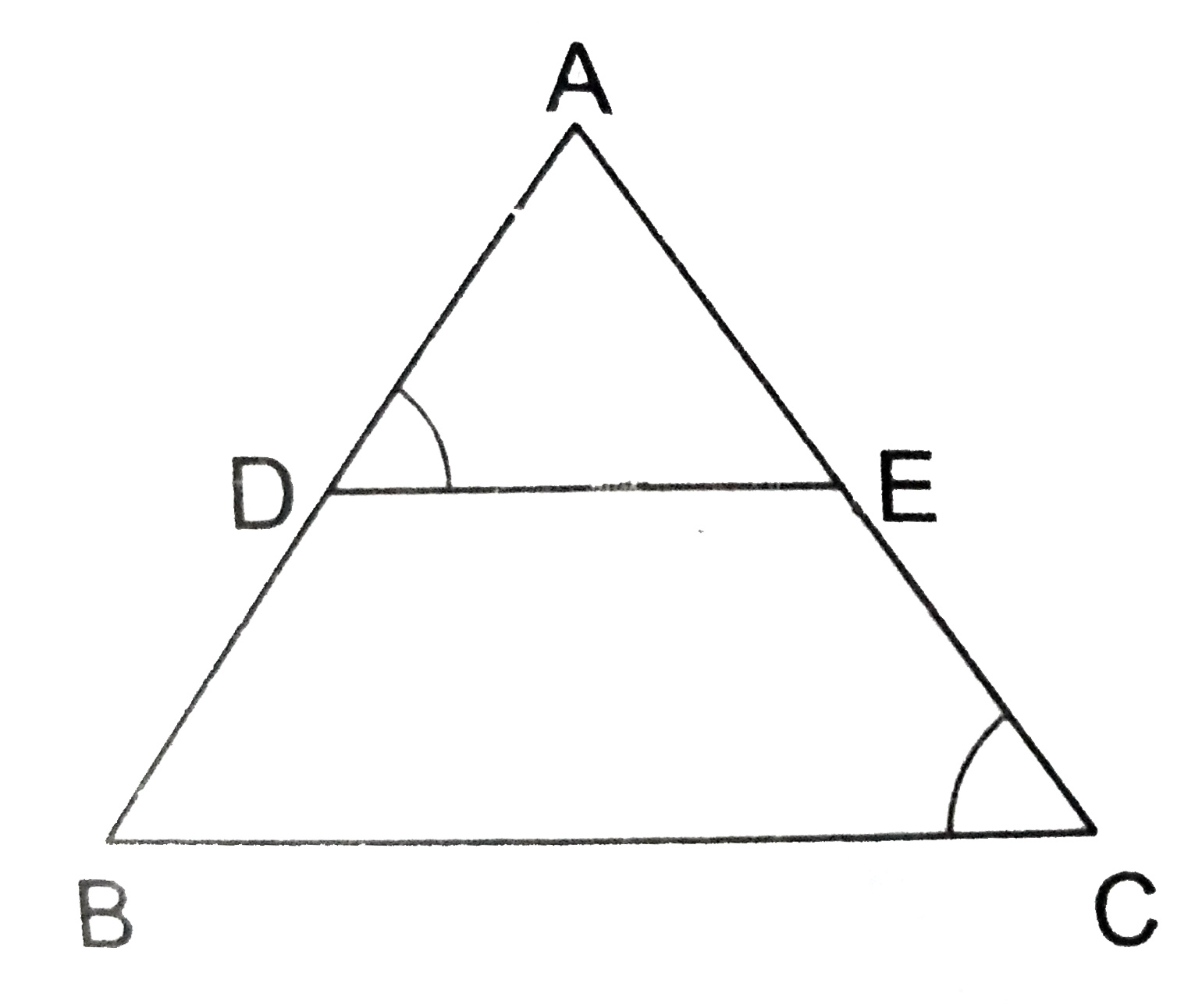
View SolutionIn the given figure, ADDB=AEEC and ∠ADE=∠ACB. Prove that ΔABC is an isosceles triangle.
 View Solution
View SolutionIn the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)
 View Solution
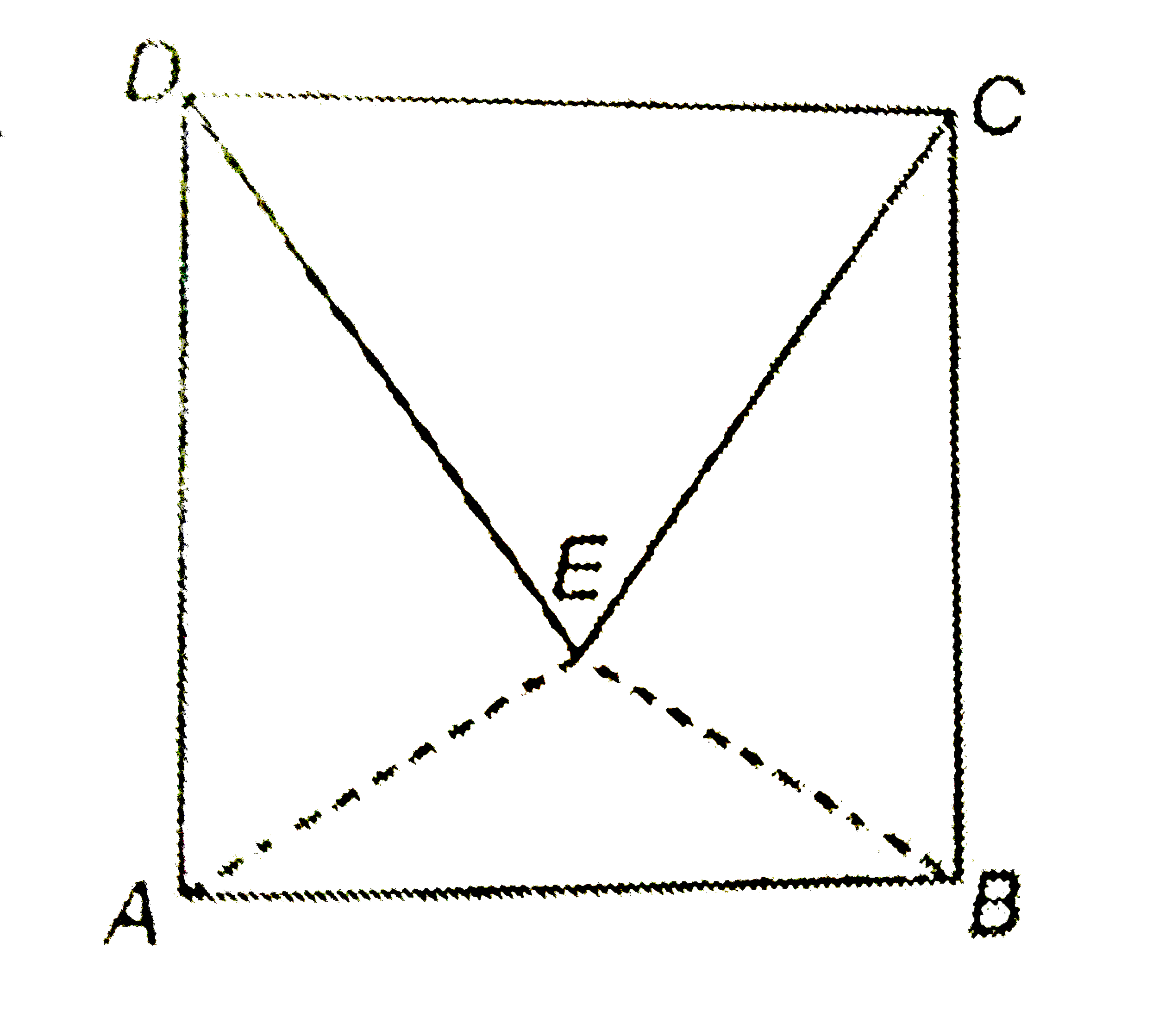
View SolutionThe adjoining figure shows a square ABCD and an equilateral triangle DEC. Prove that :
(i) ∠ADE=∠BCE=30∘
(ii) Δ≅ΔBCE
 View Solution
View SolutionThe following figure shows a square ABCD and an equilateral triangle DCE. Prove that :
(i) ∠ADE=∠BCE=150∘
(ii) ΔADE≅ΔBCE
(iii) AE=BE
 View Solution
View Solution

