एक सबहि त्रिभुज ABC में, भुजा BC, D पर समद्विभाजित है तो सिद्ध कीजिए कि, 9AD2=7AB2
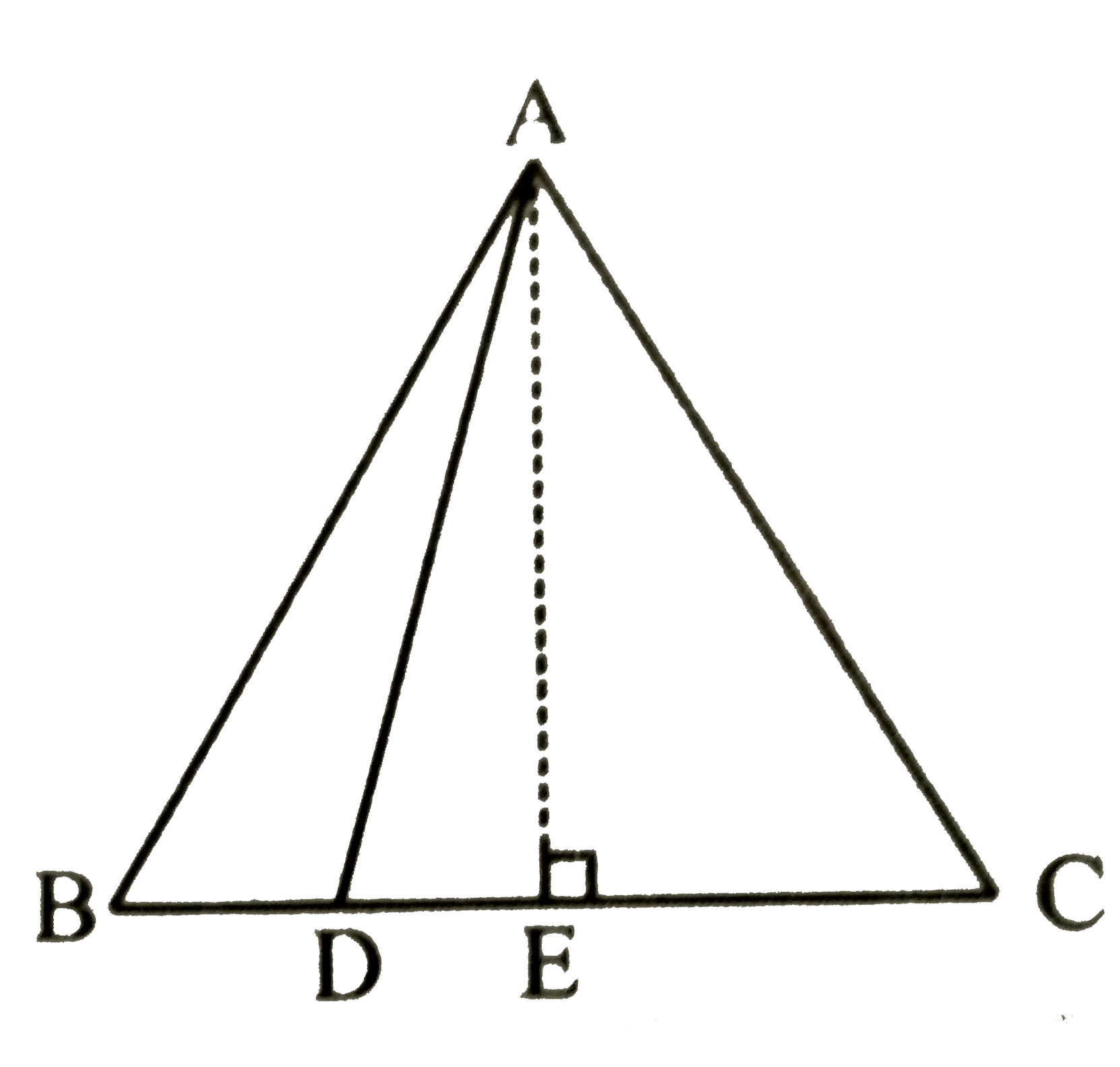
यहाँ आकृति (चित्र 1.121) में, ABC एक समबाहु त्रिभुज है तथा BC पर कोई बिन्दु D है |
तथा BD=13BC
अब AE⊥BC खींचा तथा AD को मिलाया |
अब △AEB तथा △AEC में, यहाँ AB = AC
∠AEB=∠AEC=90∘
तथा AE = AE
तब समरूपता की RHS-कसौटी द्वारा,
△AEB~△AEC⇒BE=EC
तब यहाँ BD=13BC,DC=23BC,BE+EC=12BC ...(1)
अब चूँकि ∠C=60∘⇒ADC एक न्यून त्रिभुज है तब यहाँ,
AD2=AC2+DC2−2CD⋅EC
=AC2+(23BC)2−2×23BC×12BC [समी० (1) से ]
⇒AD2=AC2+49BC2−23BC2
=AB2+49AB2−23AB2 (∵AB=BC=AC)
⇒AD2=9AB2+4AB2−6AB29=79AB2
अतः 9AD2=7AB2
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
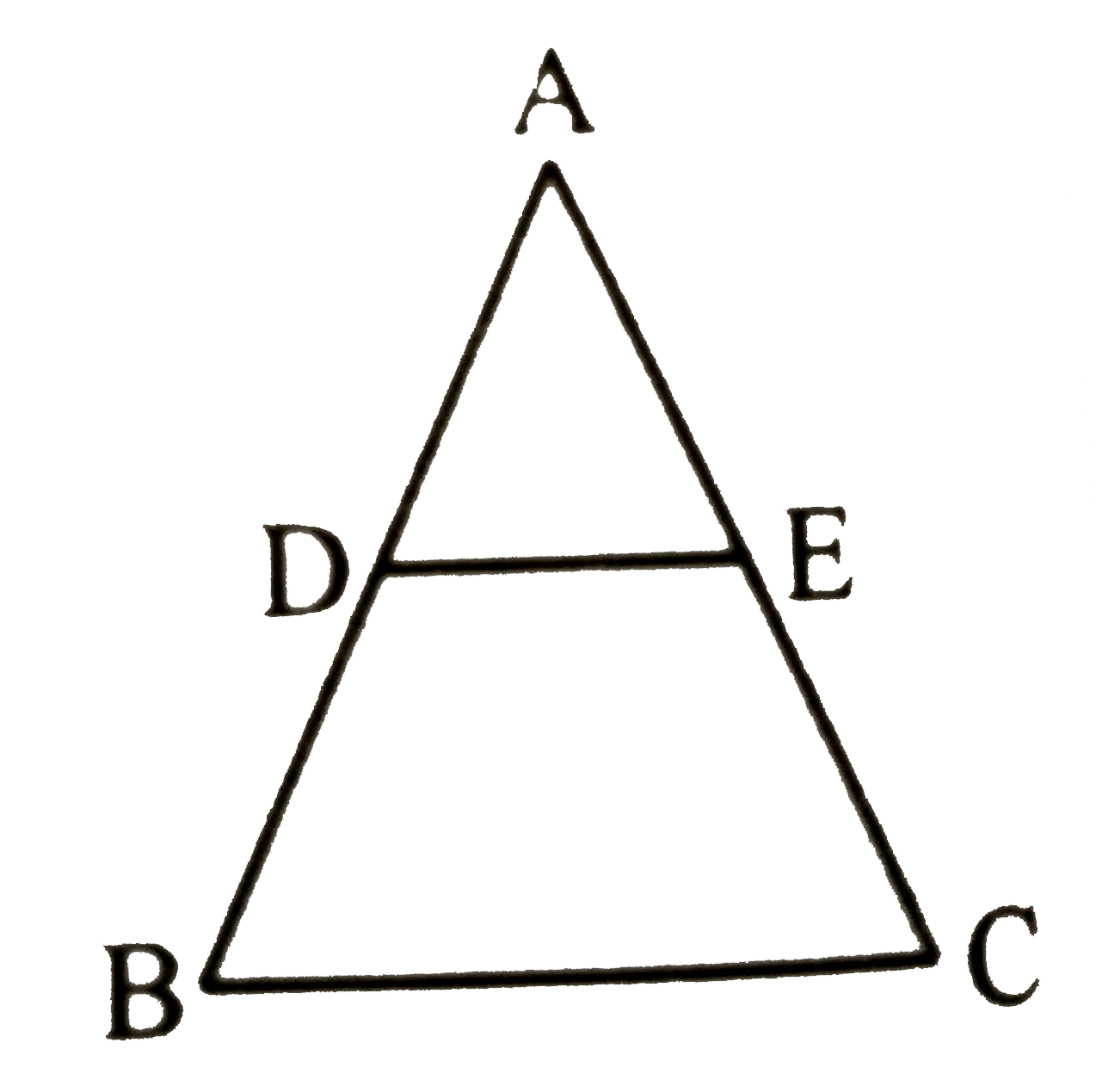
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn an equilateral triangle ABC the side BC is trisected at D . Prove that 9 AD2=7 AB2
View Solutionसमबाहु त्रिभुज ABC में भुजा BC को बिन्दु D पर त्रिभाजित किया गया है । सिद्ध कीजिए कि 9AD2=7AB2.
View SolutionIn an equilateral Triangle ABC,D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
View SolutionBD = 1/3 BC ಆಗುವಂತೆ ಸಮಬಾಹು ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ D ಯು BCಯ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. 9AD2=7AB2ಎಂದು ಸಾಧಿಸಿ.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn equilateral DeltaABC, D is a point on BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn an equilateral triangle ABC,the side BC is trisected at D.Prove that:9AD2=7AB2.
View Solutionਕਿਸੇ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC 'ਤੇ ਇਕ ਬਿੰਦੂ D ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ BD=1/3 BC ਹੈ,ਸਿੱਧ ਕਰੋ ਕਿ 9AD2=7AB2 ਹੈ।
View Solution
