In an equilateral triangle the side is trisected at . Prove that
To prove that 9AD2=7AB2 in the equilateral triangle ABC where BC is trisected at D, we can follow these steps:
Step 1: Understand the properties of the equilateral triangle
In an equilateral triangle ABC, all sides are equal, so we have:
AB=BC=CA
Step 2: Trisect the side BC
Since BC is trisected at point D, we can denote:
BD=DC=13BC
Step 3: Construct a perpendicular from A to BC
Let M be the foot of the perpendicular from A to BC. Since ABC is equilateral, AM is the altitude.
Step 4: Use the properties of triangles
In triangles AMD and AMC, both triangles share the altitude AM and have a right angle at M.
Step 5: Apply the Pythagorean theorem
For triangle AMD:
AD2=AM2+DM2
For triangle AMC:
AC2=AM2+MC2
Step 6: Express DM and MC in terms of BC
Since D is one-third of BC:
DM=13BC−12BC=16BC
And since M is the midpoint of BC:
MC=12BC
Step 7: Substitute into the equations
From the Pythagorean theorem in triangle AMD:
AD2=AM2+(16BC)2
From triangle AMC:
AC2=AM2+(12BC)2
Step 8: Relate AD2 and AB2
Since AB=AC=BC:
AB2=AM2+(12BC)2
Step 9: Set up the equations
We can now express AD2 in terms of AB2:
AD2=AM2+(16BC)2
AB2=AM2+(12BC)2
Step 10: Solve for AD2
Substituting AB2 into the equation for AD2:
AD2=AM2+136BC2
And from AB2:
AB2=AM2+14BC2
Rearranging gives:
AM2=AB2−14BC2
Step 11: Substitute back into AD2
Substituting this back into the equation for AD2:
AD2=(AB2−14BC2)+136BC2
Combine terms:
AD2=AB2−936BC2+136BC2=AB2−836BC2
Step 12: Final relationship
Now, we can express 9AD2 in terms of AB2:
9AD2=9(AB2−836BC2)
Since BC=AB:
9AD2=9AB2−2AB2=7AB2
Conclusion
Thus, we have proved that:
9AD2=7AB2
In an equilateral triangle ABC, all sides are equal, so we have:
AB=BC=CA
Since BC is trisected at point D, we can denote:
BD=DC=13BC
Let M be the foot of the perpendicular from A to BC. Since ABC is equilateral, AM is the altitude.
In triangles AMD and AMC, both triangles share the altitude AM and have a right angle at M.
For triangle AMD:
AD2=AM2+DM2
For triangle AMC:
AC2=AM2+MC2
Since D is one-third of BC:
DM=13BC−12BC=16BC
And since M is the midpoint of BC:
MC=12BC
From the Pythagorean theorem in triangle AMD:
AD2=AM2+(16BC)2
From triangle AMC:
AC2=AM2+(12BC)2
Since AB=AC=BC:
AB2=AM2+(12BC)2
We can now express AD2 in terms of AB2:
AD2=AM2+(16BC)2
AB2=AM2+(12BC)2
Substituting AB2 into the equation for AD2:
AD2=AM2+136BC2
And from AB2:
AB2=AM2+14BC2
Rearranging gives:
AM2=AB2−14BC2
Substituting this back into the equation for AD2:
AD2=(AB2−14BC2)+136BC2
Combine terms:
AD2=AB2−936BC2+136BC2=AB2−836BC2
Now, we can express 9AD2 in terms of AB2:
9AD2=9(AB2−836BC2)
Since BC=AB:
9AD2=9AB2−2AB2=7AB2
Thus, we have proved that:
9AD2=7AB2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2Dnone of theseIn an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2DNone of theseIn an equilateral triangle ABC, the side BC is trisected at D. Find the value of AD2 :
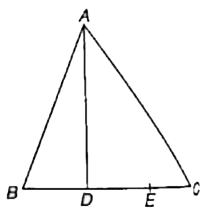 A97AB2B79AB2C34AB2D45AB2
A97AB2B79AB2C34AB2D45AB2
In an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)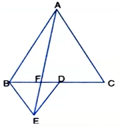
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
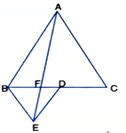
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View Solution
