(a) चित्रानुसार एक लंबे, सीधे तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लम्बाई a है के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए ।
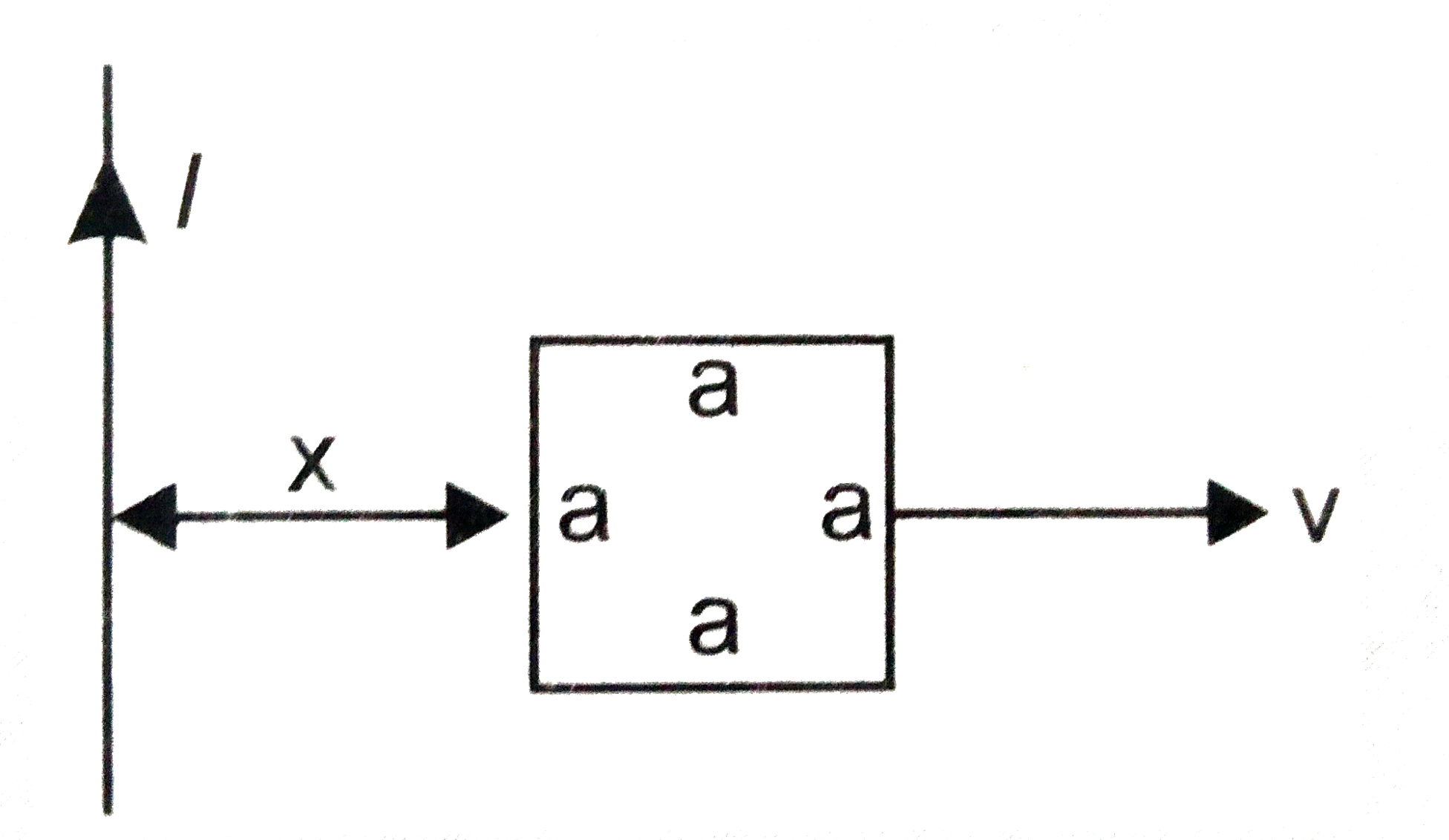
(b) अब मान लीजिए कि सीधे तार में 50 A की धारा प्रवाहित हो रही है तथा लूप एक स्थितर वेग v=10 मीटर/सेकण्ड से दायीं और गति कर रहा है लूप में प्रेरित वि. वा. बल का परिकलन उस क्षण पर कीजिए जब x=0.2 मीटर हो लूप के लिए a=0.1 मीटर लीजिये तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है
(a) माना I धारा वाले तार से x दूरी पर dx मोटाई की अल्प-पट्टी है वर्ग की भुजा a है तार से x दूरी पर चुम्बकीय क्षेत्र
B=μ04π⋅2Ix . . (i)
(अनंत लम्बाई के धारावाही तार के चुम्बकीय क्षेत्र का सूत्र प्रयुक्त करने पर, B=μ04π⋅2Ix )
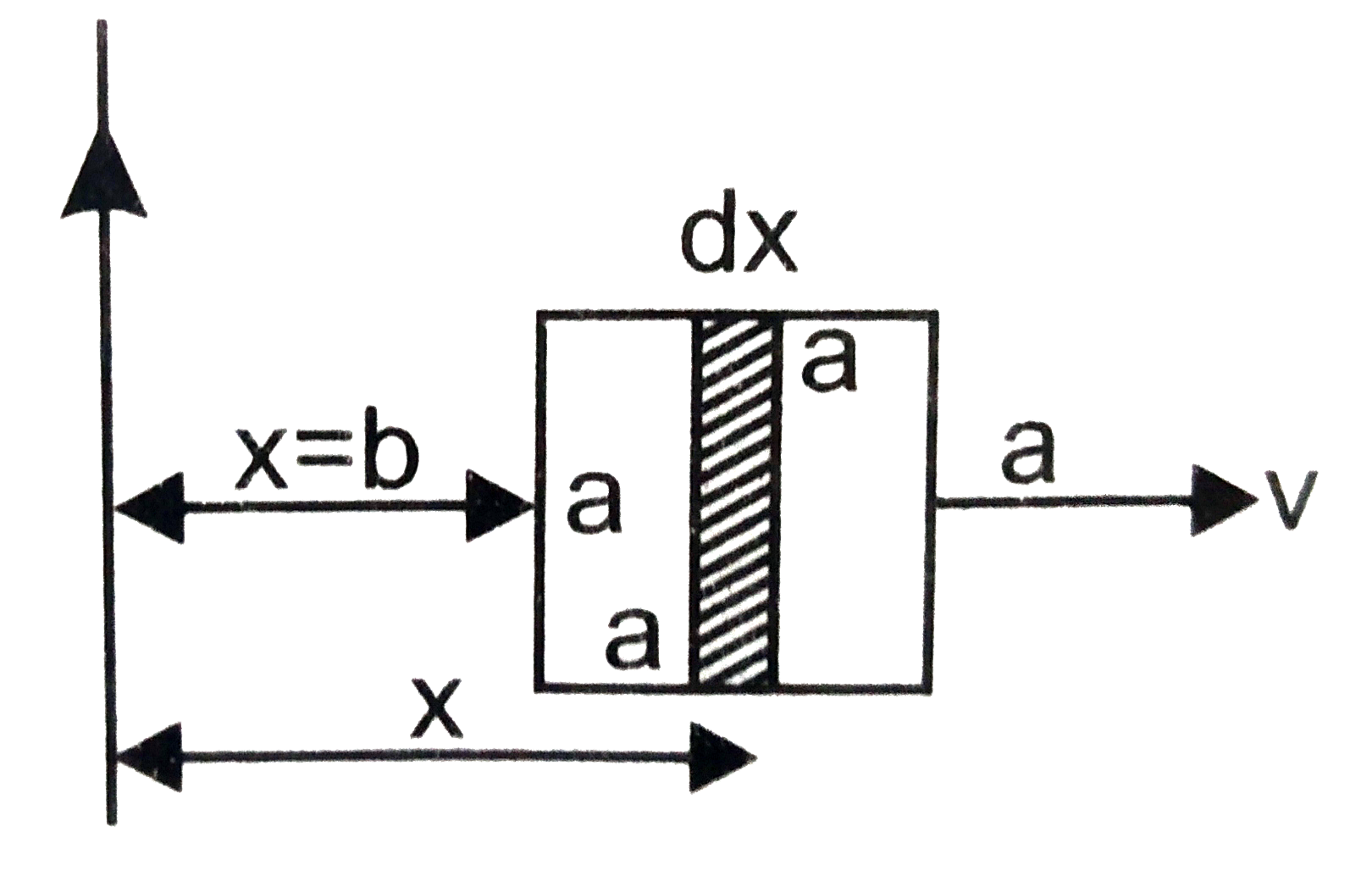
अल्प - पट्टी से होकर गुजरने वाले चुम्बकीय फ्लक्स की सूक्ष्म मात्रा,
dϕ=B.dA=μ04π⋅2Ix⋅adx
[∵dA = पट्टी का क्षेत्रफल =adx समीकरण (i) से]
dϕ=μ04π⋅Iax⋅dx
दी गई सीमाओं के अंदर समाकलन करने पर,
ϕ=μ04π⋅Ia∫(x+a)x1xdx=μ04π⋅Ia[lnx]x+ax
ϕ=μ04π⋅Ia[ln(x+a)−ln(x)]=μ0Ia2πln(x+ax)
ϕ=μ0Ia2πln(ax+1) . . . (ii)
हम जानते है कि ϕ=MI
जहाँ, M अन्योन्य प्रेरण गुणांक है
समीकरण (ii) तथा (iii) से
MI=μ0Ia2πln(ax+1)
MI=μ0a2πloge(ax+1)
अतः यह तार तथा वर्गाकार लूप के मध्य अन्योन्य प्रेरण का सम्बन्ध है
(b) दिया है- धारा (I)=50A
वेग (v)=10 मीटर/सेकण्ड
x=0.2 मीटर तथा a=0.1 मीटर
प्रेरित वि. वा. बल
e=−dϕdt=−ddt[Iμ0a2πloge(a+xx)]
=−μ0aI2πdx[log(x+1)−logx]
=−μ0aI2π[1(x+1)ddt(x+1)−1xddt(x)]
=−μ0aI2π[1(x+1)dxdt−1xdxd] [∵dxdt=v]
=−μ0aI2π[v(x+a)−vx]
e=μ02π⋅a2Ivx(a+x)
e=−4π×10−72π×(0.1)2×(50)×(10)0.2×(0.1+0.2)
=2×10−7×50×10−2×100.2×0.3
=1.67×10−5V
Topper's Solved these Questions
- वैधुत चुम्बकीय प्रेरण BOOK - BALAJI PUBLICATIONCHAPTER - वैधुत चुम्बकीय प्रेरण EXERCISE - NCERT पाठ्य-पुस्तक के हल
10 Videos
- वैधुत आवेश तथा क्षेत्रBOOK - BALAJI PUBLICATIONCHAPTER - वैधुत आवेश तथा क्षेत्रEXERCISE - NCERT पाठ्य-पुस्तक के हल
31 Videos
- संचार व्यवस्था BOOK - BALAJI PUBLICATIONCHAPTER - संचार व्यवस्था EXERCISE - NCERT पाठ्य -पुस्तक के हल
8 Videos
Similar Questions
चित्र (a) से (f) में वर्णित स्थितियों के लिए प्रेरित धारा की दिशा की प्रागुक्ति (predict) कीजिए
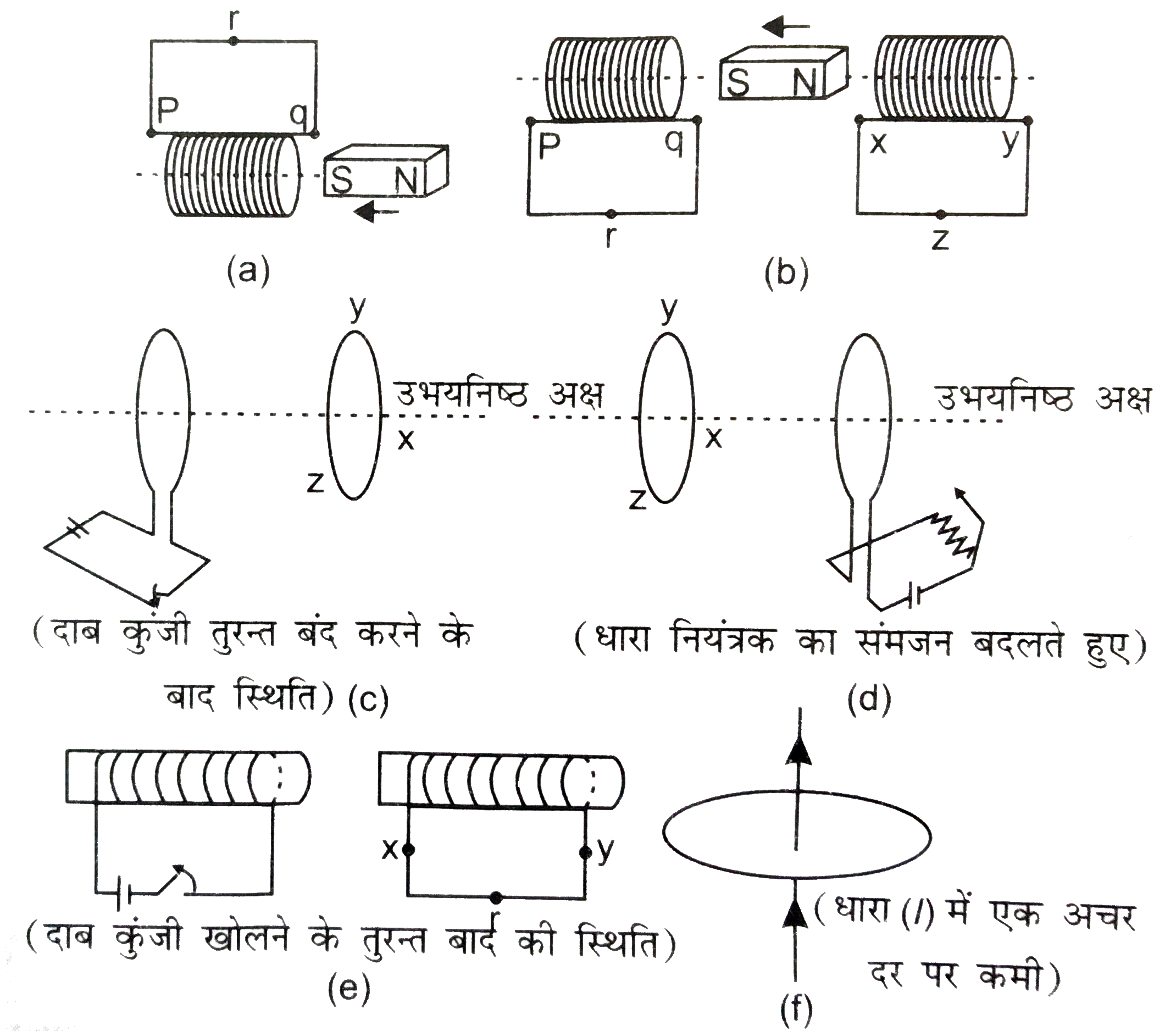
View Solutionवायु के एक-दूसरे से 30 सेमी दूरी पर रखे दो छोटे आवेशित गोलों पर क्रमश: 2×10−7C तथा 3×10−7C आवेश है, उनके बीच कितना बल है?
View Solutionव्योम तरंगों के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित आवृत्तियों में से कौन-सी उपयुक्त रहेगी ?
View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionएक स्थिर आयतन वाले खुले टैंक का आधार वर्गाकार है। यदि अंत: पृष्ठ न्यूनतम हो, तब टैंक कि गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionउस बड़े से बड़े गोले का आयतन ज्ञात कीजिए, जो उस घन में से काटा गया जिसकी एक भुजा की लम्बाई 4 सेमी है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solution
