किसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिए कि किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान है । पहिए के स्पोक (slope) हलके एवं कुचालक है तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतन्त्र है जैसाकि चित्र में दर्शाया गया है पहिए के वृत्तियाँ भाग पर रिम के अंदर एकसमान चुम्बकीय क्षेत्र विस्तारित है इसे निम्न प्रकार परिभाषित किया गया है ।
= 0 (अन्यथा)
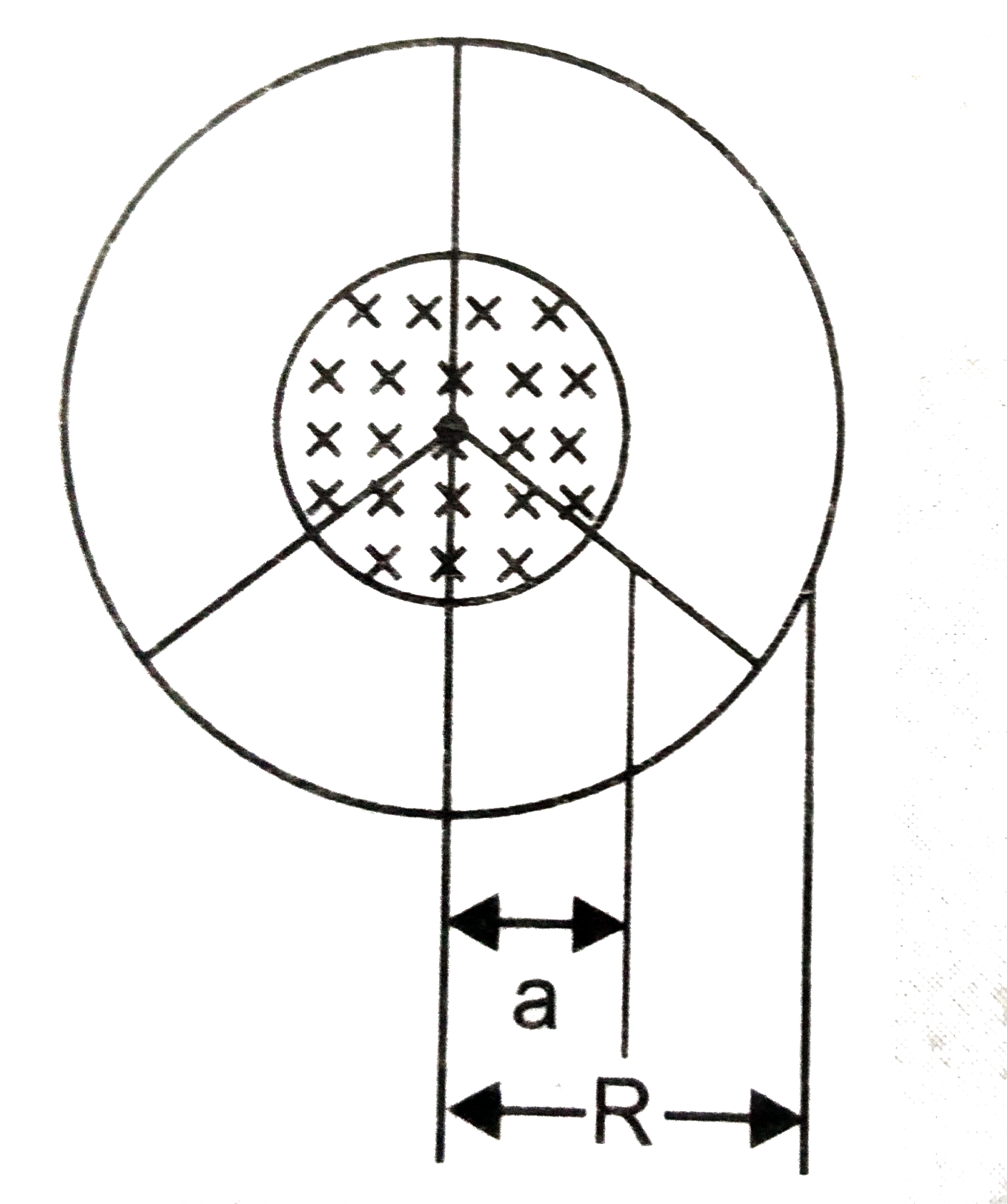
चुम्बकीय क्षेत्र को अचानक 'ऑफ़' (switched off) करने के पश्चात पहिए का कोणीय वेग ज्ञात कीजिए ?
दिया है- रेखीय आवेश घनत्व
. . (i)
रिम की त्रिज्या =R रिम का द्रव्यमान =m
वृत्तीय क्षेत्र के बाहर चुम्बकीय क्षेत्र,
=0 (अन्यथा)
माना व्हील का कोणीय वेग है तब
प्रेरित वि. वा. बल
अतः वैधुत क्षेत्र तथा वैधुत फ्लक्स परिवर्तन की दर के मध्य सम्बन्ध,
चुम्बकीय फ्लक्स में परिवर्तन के कारण E, त्रिज्या की परिधि के अनुदिश अवस्थित है
आवेश पर बल
किन्तु बल
दोनों ओर समाकलन करने पर,
चूँकि कोणीय वेग की दिशा अक्षो के अनुदिश है
Topper's Solved these Questions
- वैधुत चुम्बकीय प्रेरण BOOK - BALAJI PUBLICATIONCHAPTER - वैधुत चुम्बकीय प्रेरण EXERCISE - NCERT पाठ्य-पुस्तक के हल
10 Videos
- वैधुत आवेश तथा क्षेत्रBOOK - BALAJI PUBLICATIONCHAPTER - वैधुत आवेश तथा क्षेत्रEXERCISE - NCERT पाठ्य-पुस्तक के हल
31 Videos
- संचार व्यवस्था BOOK - BALAJI PUBLICATIONCHAPTER - संचार व्यवस्था EXERCISE - NCERT पाठ्य -पुस्तक के हल
8 Videos
Similar Questions
चित्र (a) से (f) में वर्णित स्थितियों के लिए प्रेरित धारा की दिशा की प्रागुक्ति (predict) कीजिए
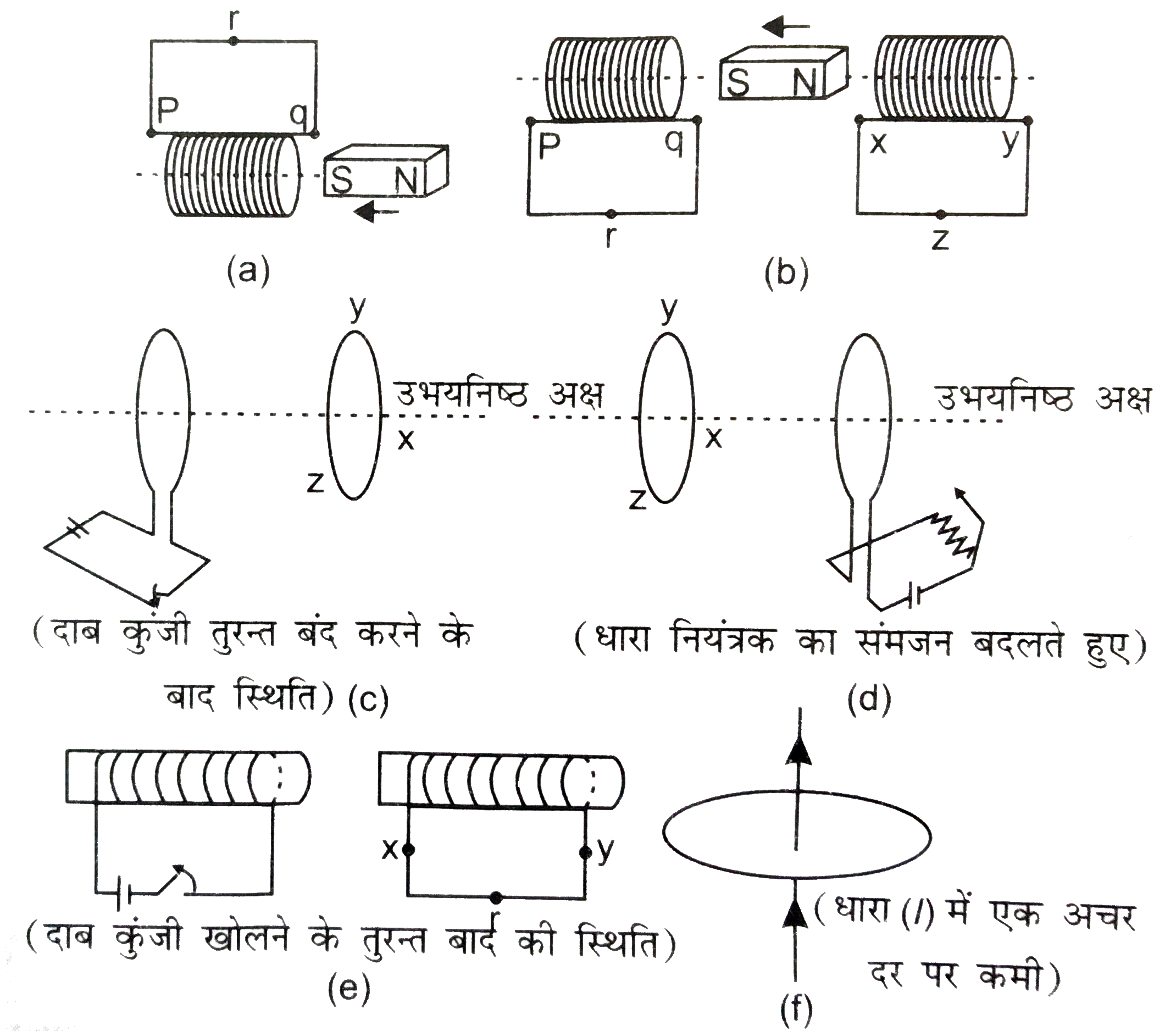
View Solutionवायु के एक-दूसरे से 30 सेमी दूरी पर रखे दो छोटे आवेशित गोलों पर क्रमश: 2×10−7C तथा 3×10−7C आवेश है, उनके बीच कितना बल है?
View Solutionव्योम तरंगों के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित आवृत्तियों में से कौन-सी उपयुक्त रहेगी ?
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solution
