The metre is defined as the distance travelled by ligh in 1299,792,458 second. Why didn't people choose some easier number such as 1300.000.000 second?
To understand why the metre is defined as the distance light travels in 1299,792,458 seconds rather than a simpler fraction like 1300,000,000 seconds, we can break down the reasoning as follows:
Step 1: Understanding the Speed of Light
The speed of light in a vacuum is approximately 299,792,458 meters per second. This value is a fundamental constant in physics and is crucial for many scientific calculations.
Step 2: Definition of the Metre
The metre is defined based on the distance light travels in a specific time interval. By defining the metre in terms of the speed of light, we ensure that it is based on a universal constant rather than a physical object, which can change over time.
Step 3: Precision in Measurement
Using 1299,792,458 seconds allows for a very precise definition of the metre. If we were to use 1300,000,000 seconds, it would introduce a small error in the measurement of the metre. The difference between these two values is significant when considering the precision required in scientific measurements.
Step 4: Historical Context
The definition of the metre has evolved over time. Before the current definition, the metre was based on physical objects (like a metal bar). The transition to a definition based on the speed of light reflects a shift towards more stable and reproducible standards.
Step 5: Conclusion
In conclusion, the choice of 1299,792,458 seconds is not arbitrary; it is based on the actual speed of light, ensuring precision and consistency in measurements across different contexts and applications.
---
The speed of light in a vacuum is approximately 299,792,458 meters per second. This value is a fundamental constant in physics and is crucial for many scientific calculations.
The metre is defined based on the distance light travels in a specific time interval. By defining the metre in terms of the speed of light, we ensure that it is based on a universal constant rather than a physical object, which can change over time.
Using 1299,792,458 seconds allows for a very precise definition of the metre. If we were to use 1300,000,000 seconds, it would introduce a small error in the measurement of the metre. The difference between these two values is significant when considering the precision required in scientific measurements.
The definition of the metre has evolved over time. Before the current definition, the metre was based on physical objects (like a metal bar). The transition to a definition based on the speed of light reflects a shift towards more stable and reproducible standards.
In conclusion, the choice of 1299,792,458 seconds is not arbitrary; it is based on the actual speed of light, ensuring precision and consistency in measurements across different contexts and applications.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 16videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 23videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Worked Out Examples10videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE1videos
HEAT TRANSFER
- BOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercises62videos
KINETIC THEORY OF GASES
Similar Questions
The speed of a car increases uniformly from zero to 10ms−1 in 2s and then remains constant (figure)

a. Find the distance travelled by the car in the first two seconds.
b. Find the distance travelled by the car in the next two seconds.
c. Find the total distance travelled in 4s.View SolutionFigure here gives the speed-time graph for a body. The displacement travelled between t = 1.0 second and t = 7.0 second is nearest to
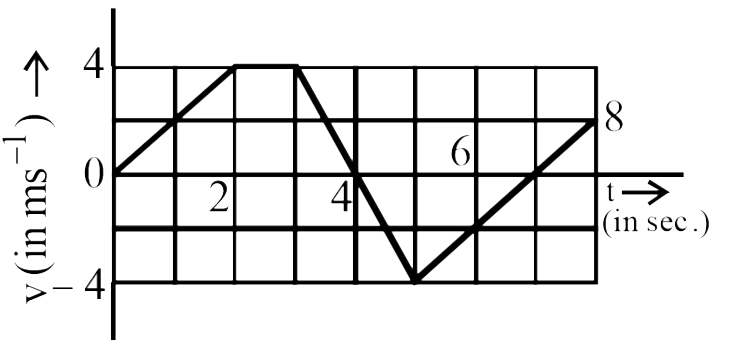 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Light travels with a speed of 3×108ms−1. The distance travelled by light in 1 femto second is
A0⋅03mmB0⋅003mmC3mmD0⋅0003mm - Question 2 - Select One
A freely falling body travelled x m in nth second. Then distance travelled in n−1th second is
AxBx + gCx -gD2x + 3g - Question 3 - Select One
If the distance 's' metres travelled by a particle in t seconds is given by s=t3−3t2, then the acceleration is zero (in m/s) is
A3B−2C−3D2
Use integeration technique to prove that the distance travelled in nth second: snth=u+a2(2n−1)
View SolutionA gun is fired at a distance of 1.7 km from Ram and he hears the sound after 25 seconds. The speed of sound in metres per second is :
View SolutionThe distance s (in cm) travelled by a particle in t seconds is given by, s=t3+2t2+t. The speed of the particle after 1s will be :
View SolutionThe distance s (in cm) travelled by a particle in t seconds is given by, s=t3+2t2+t. The speed of the particle after 1s will be :
View SolutionThe distance travelled s in metres by a particle in t second is given by s=t3+2t2+t. The speed of the particle after 1s will be
View Solution

