Find the dimensions of
a. electric field E,
magnetic field B and
magnetic permeability
. The relavant equations are
where F is force q is charge, is speed I is current, and is distance.
The correct Answer is:A, B, C
(a) Electric field
(b) Magnetic field
(c) megnetic permeability
= ([MT^-2 I^-1] xx[L])/([I]) = [MLT^-2 i^-2]
Topper's Solved these Questions
Similar Questions
The dimension of B22μ0, where B is magnetic field and μ0 is the magnetic permeability of vacuum, is :
View SolutionFind the dimensions of
a. electric dipole moment p and
b. magnetic dipole moment M.
The defining equations are p=q.dandM=IA,
whre d is distance, A is area, q is charge and I is current.
View Solution
Knowledge Check
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)E2μ0 has the dimensions (E= electric field, μ0= permeabililty of free space)
A[M2L3T−2A2]B[MLT−4]C[ML3T−2]D[M−1L2TA−2]An electric charge q is moving with a velocity w in the direction of a magnetic field B. The magnetic force acting on the charge is
AqvBBzeroCqvBDvqB
Energy density in the electric field of electromagnetic wave is U.If amplitude of electric field (E0) and magnetic field (B0) is related as E0=cB0, then energy density in magnetic field is(c = speed of light)
View SolutionWhat is dimensional formulae of magnetic field (B) if F=qvB sinθ, where F is magnitude of force, q is charge , v is speed and B is magnetic field and θ is angle between velocity and magnetic field.
View SolutionThe dimensions of B2R2C22μ0 (Where B is magnetic filed, and μ0 is permeability of free space , R resistance and C is capacitance) is
View SolutionWhat is dimensional formulae of magnetic field (B) if F=qvBsinθ, where F is magnitude of force, q is change, v is speed and B is magnetic field and θ is angle between velocity and magnetic field.
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
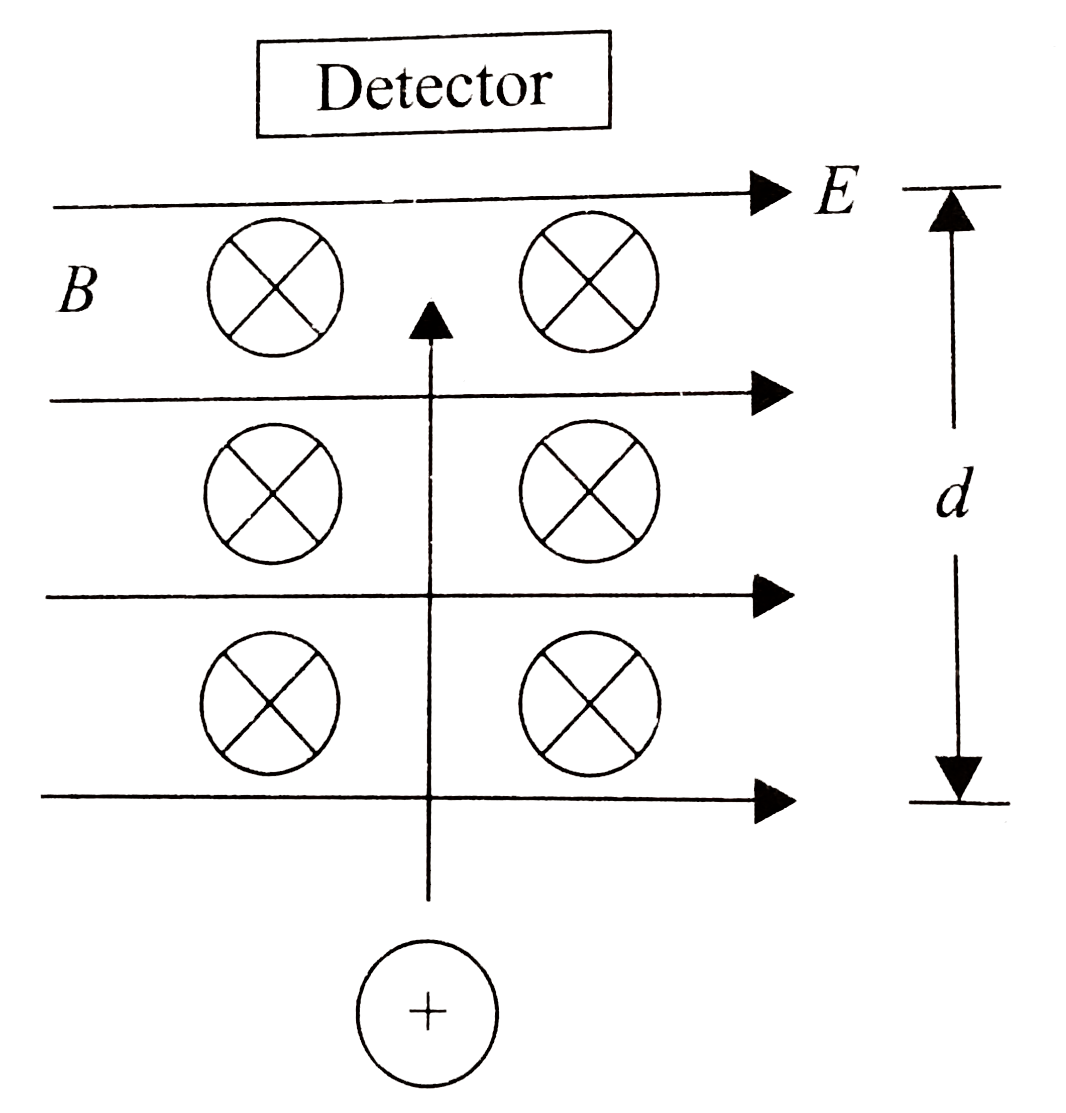
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View Solution
