विद्युत - क्षेत्र में आवेश q पर आरोपित बल परिणामी एंव दिशा में सूत्र व्दारा व्यक्त होता हैं । आरोपित बल की दिशा आवेश की प्रकृति ( धनात्मक एंव ऋणात्मक ) पर निर्भर करती हैं । स्प्ष्टतः , किसी एकसमान विद्युत - क्षेत्र ( uniform electric field ) में विराम में स्थित मुक्त आवेश क्षेत्र की दिशा के समांतर अथवा विपरीत दिशा में सरल रेखा में गतिशील होता हैं । यदि कोई गतिशील आवेशित कण विद्युत - क्षेत्र की दिशा के साथ कोण बनाता हुआ क्षेत्र में प्रवेश करता हो तब इसका गति पथ परवलीय (parabolic) होता हैं , यदि .
इसी क्रम में क्षैतिज दिशा में गतिशील प्रोटॉन पर विचार करें जो समय t = 0 पर एकसमान ऊर्ध्वाधर विद्युत - क्षेत्र (uniform vertical electric field) में प्रवेश कर रहा हो । प्रवेश करते समय जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र की उपस्थिति में प्रोटॉन को जमीन (ground) से इसकी ऊँचाई h हैं । प्रेक्षण से ज्ञात होता हैं कि क्षेत्र की उपस्थिति में प्रोटॉन को जमीन तक आने में लगा समय , क्षेत्र की अनुपस्थिति में लगनेवाले समय का आधा हैं । यह भी पाया जाता हैं कि क्षेत्र के अंदर प्रोटॉन व्दारा ( माइक्रोसेकंड) में 10 cm का क्षैतिज विस्थापन होता हैं और अंततः यह की चाल से जमीन से टकराता हैं ।
जमीन से टकराते समय प्रोटॉन के वेग का ऊर्ध्वाधर घटक (vertical component ) हैं ।
The correct Answer is:C
क्षेत्र की उपस्थिति में समय का मान आधा होने का अर्थ हैं त्वरण g' का मान g का चार गुना होना । स्पष्टतः , अतिरिक्त त्वरण = 3g , अतः की दिशा ऊर्ध्वाधरतः नीचे की ओर होगी । ऊर्ध्वाधर त्वरण के कारण वेग का क्षैतिज घटक का मान अपरिवर्तित रहेगा । फिर , टकराने समय . यहाँ प्रश्न से , तथा . अतः , वेग का ऊर्ध्वाधर घटक, .
अब गति के ऊर्ध्वाधर घटक के लिए ,
या .
अतः , अभीष्ट समय , .
Topper's Solved these Questions
Similar Questions
केथोड किरणों के लिए निम्नांकित में क्या सत्य है?
View Solutionकॉलम A में दी गई भौतिक राशियों को कॉलम B में व्यक्ति उनके संगत SI मात्रक के बीच मेल स्थापित करे ।
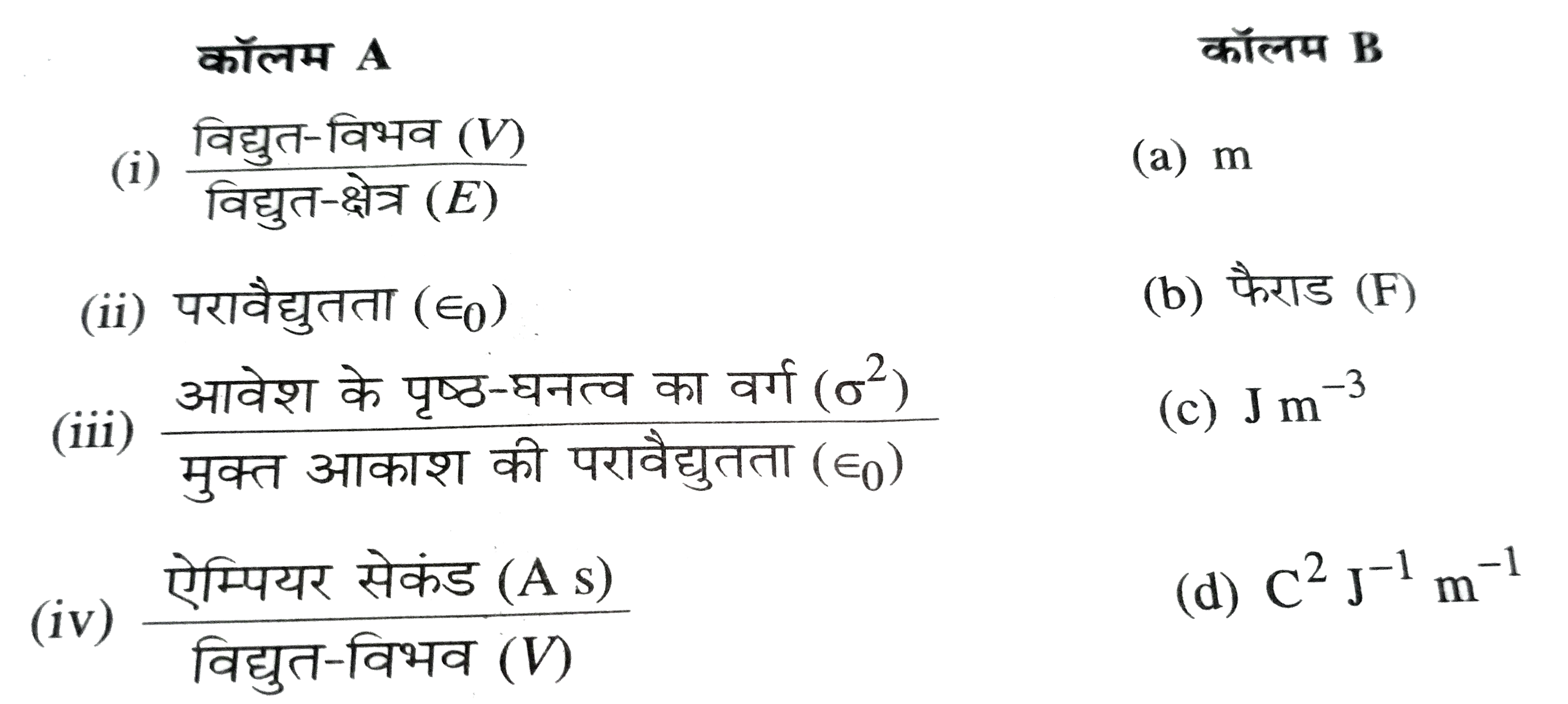
View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionचुम्बकीय क्षेत्र में आवेश की गति
View Solutionचुंबकीय क्षेत्र में किसी विद्युत धारावाही चालक पर बल
View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionविद्युत धारावाही चालक पर चुंबकीय बल | दो समांतर विद्युत धाराओं के बीच बल-ऐम्पियर | एकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solutionएकसमान चुम्बकीय क्षेत्र में गतिमान आवेश (2)
View Solutionएकसमान क्षेत्र मे गतिमान आवेश की गति
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionबिंदु आवेश के कारण वैद्युत क्षेत्र की तीरवता|वैद्युत बल रेखाएँ|एकसमान तथा असमान वैद्युत क्षेत्र में वैद्युत बल रेखाएं|OMR
View Solutionगतिमान आवेश की चुंबकीय क्षेत्र में गति
View Solutionकूलॉम के नियम पर महत्वपूर्ण उदाहरण |विद्युत क्षेत्र |विद्युत क्षेत्र की दिशा |विद्युत बल एवं विद्युत क्षेत्र मे संबंध | विद्युत क्षेत्र का अध्यारोपण |OMR|Summary
View Solutionचुंबकीय और विद्युत क्षेत्र में आवेश | लोरेंत्ज़ बल
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solution
