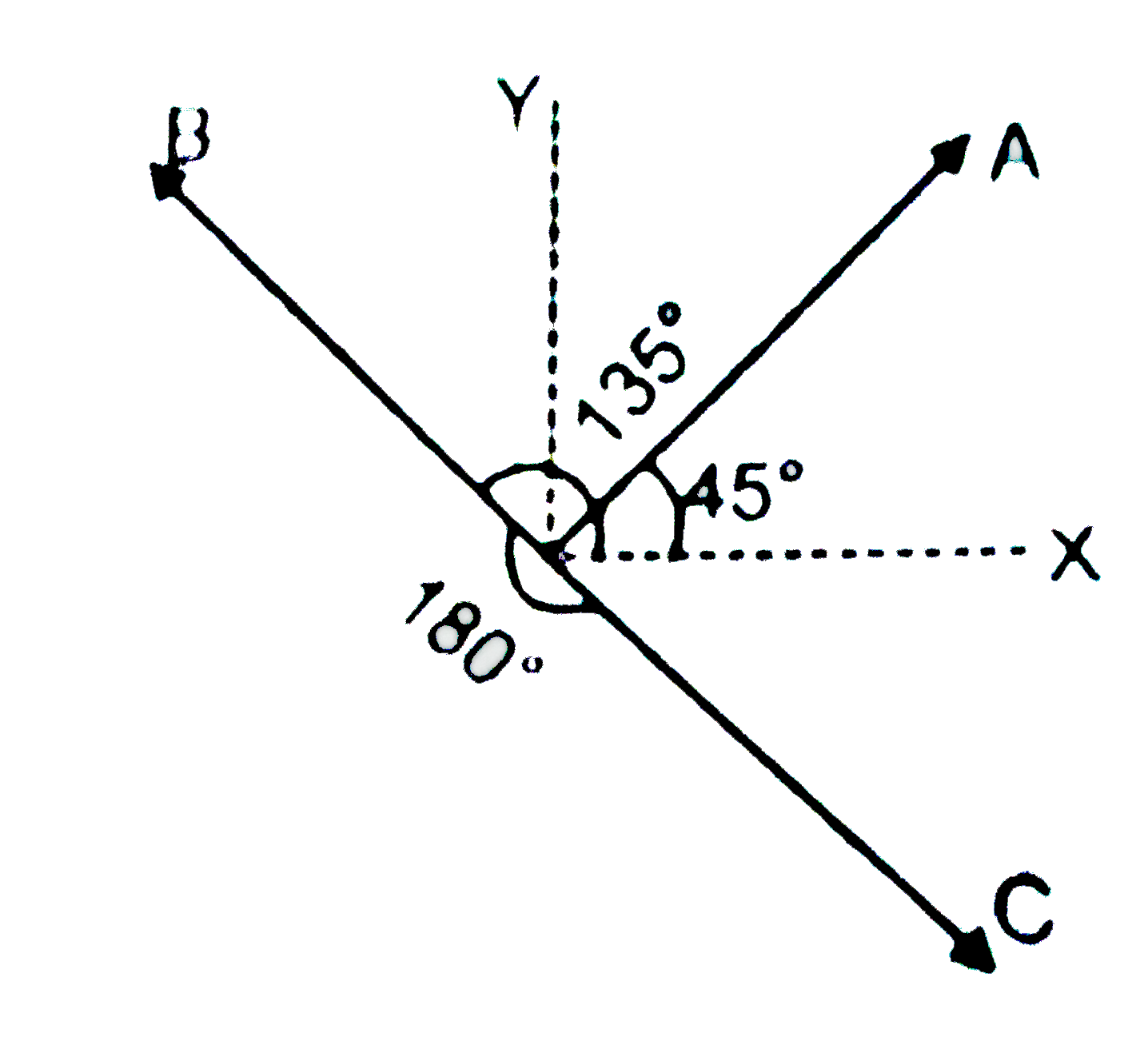
Add vectors $\vec{A}, \vec{B} and \vec{C}$ each having magnitude of 100 unit and inclined to the X-axis at angles $45^{\circ}, 135^{\circ} and 315^{\circ}$ respectively.

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:100 unit at $45^{\circ}$ with x axis

To solve the problem of adding vectors $\to A$ , $\to B$ , and $\to C$ with given magnitudes and angles, we will follow these steps:
Step 1: Determine the components of each vector
1. Vector $\to A$ :
- Magnitude: 100 units
- Angle: $45^{\circ}$
- Components:
${\to A}_{x} = 100 cos (45^{\circ}) = 100 \cdot \frac{1}{\sqrt{2}} = 50 \sqrt{2}$
${\to A}_{y} = 100 sin (45^{\circ}) = 100 \cdot \frac{1}{\sqrt{2}} = 50 \sqrt{2}$
2. Vector $\to B$ :
- Magnitude: 100 units
- Angle: $135^{\circ}$
- Components:
${\to B}_{x} = 100 cos (135^{\circ}) = 100 \cdot (- \frac{1}{\sqrt{2}}) = - 50 \sqrt{2}$
${\to B}_{y} = 100 sin (135^{\circ}) = 100 \cdot \frac{1}{\sqrt{2}} = 50 \sqrt{2}$
3. Vector $\to C$ :
- Magnitude: 100 units
- Angle: $315^{\circ}$
- Components:
${\to C}_{x} = 100 cos (315^{\circ}) = 100 \cdot \frac{1}{\sqrt{2}} = 50 \sqrt{2}$
${\to C}_{y} = 100 sin (315^{\circ}) = 100 \cdot (- \frac{1}{\sqrt{2}}) = - 50 \sqrt{2}$
Step 2: Sum the components of the vectors
Now we will add the components of the three vectors:
- Total $x$ -component:
$R_{x} = {\to A}_{x} + {\to B}_{x} + {\to C}_{x} = 50 \sqrt{2} - 50 \sqrt{2} + 50 \sqrt{2} = 50 \sqrt{2}$
- Total $y$ -component:
$R_{y} = {\to A}_{y} + {\to B}_{y} + {\to C}_{y} = 50 \sqrt{2} + 50 \sqrt{2} - 50 \sqrt{2} = 50 \sqrt{2}$
Step 3: Calculate the magnitude of the resultant vector
The magnitude of the resultant vector $\to R$ can be calculated using the Pythagorean theorem:
$R = \sqrt{R_{x}^{2} + R_{y}^{2}} = \sqrt{(50 \sqrt{2})^{2} + (50 \sqrt{2})^{2}} = \sqrt{5000 + 5000} = \sqrt{10000} = 100$
Step 4: Determine the direction of the resultant vector
The direction (angle $θ$ ) can be found using:
$tan (θ) = \frac{R_{y}}{R_{x}} = \frac{50 \sqrt{2}}{50 \sqrt{2}} = 1$
Thus,
$θ = 45^{\circ}$
Final Result
The resultant vector $\to R$ has a magnitude of 100 units and is inclined at an angle of $45^{\circ}$ to the x-axis.
---

|

Updated on:7/8/2024

Class 11 PHYSICS BASIC MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to a and \to b$ are unit vectors inclined to x-axis at angle $30^{\circ} and 120^{\circ}$ then $∣ ∣ \to a + \to b ∣ ∣$ equals
A $\sqrt{2 / 3}$
B $\sqrt{2}$
C $\sqrt{3}$
D2
Question 2 - Select One
The vector sum of three vectors $\to A, \to B$ and $\to C$ is zero . If $ˆ i$ and $ˆ j$ are the unit vectores in the vectors in the directions of $\to A$ and $\to B$ respectively , them :
A $\to C$ is in the plane of $ˆ i$ of $ˆ j$
B $\to C$ is along $ˆ i \times ˆ j$
C $\to C$ is along $ˆ i$
D $\to C$ is along $ˆ j$
Question 3 - Select One
A magnitude of vector $\to A, \to B$ and $\to C$ are respectively $12, 5$ and $13$ units and $\to A + \to B = \to C$ then the angle between $\to A$ and $\to B$ is
A $0$
B $π$
C $π / 2$
D $π / 4$

HC VERMA-PHYSICS AND MATHEMATICS-Exercises

Home
Ask Doubt
Profile