Two particles A and B starts from rest and move for equal time on a straight line. The particle A has an acceleration a for the first of the total time and 2a for the second half. The particle B has an acceleration 2a for the first half and a for the second half. Which particle has covered larger distance?
To solve the problem, we need to analyze the motion of both particles A and B over the same time interval, t. We will calculate the distance covered by each particle in two halves of the time interval, as specified in the question.
1. Define the Time Intervals:
- Let the total time be t.
- The first half of the time interval is t2 and the second half is also t2.
2. Calculate the Distance Covered by Particle A:
- First Half (Acceleration = a):
- Initial velocity u=0.
- Using the equation of motion:
x1=ut+12at2=0+12a(t2)2=12a⋅t24=at28
- Second Half (Acceleration = 2a):
- The final velocity at the end of the first half is:
v=u+at=0+a⋅t2=at2
- Now, using the equation of motion for the second half:
x2=ut+12at2=(at2)⋅t2+12(2a)(t2)2
=at24+12⋅2a⋅t24=at24+at24=2at24=at22
- Total Distance Covered by A:
dA=x1+x2=at28+at22=at28+4at28=5at28
3. Calculate the Distance Covered by Particle B:
- First Half (Acceleration = 2a):
- Initial velocity u=0.
- Using the equation of motion:
x1=ut+12at2=0+12(2a)(t2)2=12⋅2a⋅t24=at24
- Second Half (Acceleration = a):
- The final velocity at the end of the first half is:
v=u+at=0+2a⋅t2=at
- Now, using the equation of motion for the second half:
x2=ut+12at2=(at)⋅t2+12a(t2)2
=at⋅t2+12a⋅t24=at22+at28=4at28+at28=5at28
- Total Distance Covered by B:
dB=x1+x2=at24+5at28=2at28+5at28=7at28
4. Comparison of Distances:
- Distance covered by A: dA=5at28
- Distance covered by B: dB=7at28
Since dB>dA, particle B has covered a larger distance than particle A.
Conclusion:
Particle B has covered a larger distance than particle A.
- Let the total time be t.
- The first half of the time interval is t2 and the second half is also t2.
- First Half (Acceleration = a):
- Initial velocity u=0.
- Using the equation of motion:
x1=ut+12at2=0+12a(t2)2=12a⋅t24=at28
- The final velocity at the end of the first half is:
v=u+at=0+a⋅t2=at2
- Now, using the equation of motion for the second half:
x2=ut+12at2=(at2)⋅t2+12(2a)(t2)2
=at24+12⋅2a⋅t24=at24+at24=2at24=at22
dA=x1+x2=at28+at22=at28+4at28=5at28
- First Half (Acceleration = 2a):
- Initial velocity u=0.
- Using the equation of motion:
x1=ut+12at2=0+12(2a)(t2)2=12⋅2a⋅t24=at24
- The final velocity at the end of the first half is:
v=u+at=0+2a⋅t2=at
- Now, using the equation of motion for the second half:
x2=ut+12at2=(at)⋅t2+12a(t2)2
=at⋅t2+12a⋅t24=at22+at28=4at28+at28=5at28
dB=x1+x2=at24+5at28=2at28+5at28=7at28
- Distance covered by A: dA=5at28
- Distance covered by B: dB=7at28
Particle B has covered a larger distance than particle A.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 1
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Worked Out Examples
20 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionA particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
View Solution
Knowledge Check
Two particles P and Q start from rest and move for equal time on a straight line. Particle P has an acceleration of Xm/s2 for the first half of the total time and 2Xm/s2 for the second half. The particle Q has an acceleration of 2Xm/s2 for the first half of the total time and Xm/s2 for the second half. Which particle has covered longer distance ?
Aboth have covered the same distanceBP has covered the larger distanceCQ has covered the larger distanceDnone of theseA body start from rest and moves in a straight line with uniform acceleration F , the distances covered by in it second , fourth and eights seconds are
Ain arthmetic progressionBin geometrical progressionCin the ratio 1:3:7Din the ratio 3:7:15A particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is
A12kt2B12at2C16at2DNone
A particle starts from rest and moves along a straight line with uniform acceleration. The ratio of distance travelled by the particle during the first three seconds to the distance travelled by the particle during the next three seconds is 3 о 2
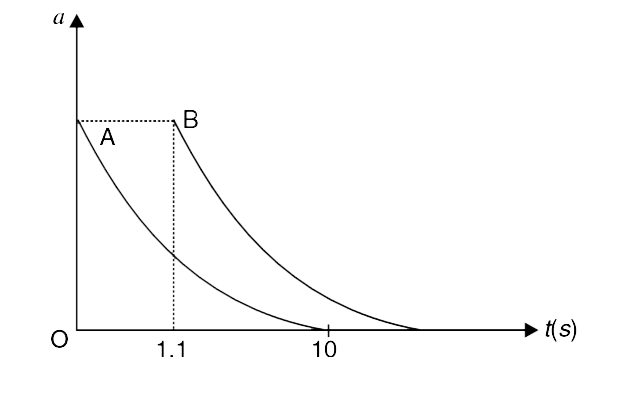
View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

View SolutionA particle starts from rest at t=0 and moves along a straight line with a variable acceleration given by a (t)=(3t+1)ms−2 ,where t],[ is in seconds.The velocity of the particle at t=4s is
View SolutionA particle at rest starts moving in a horizontal straight line with a uniform acceleration. The ratio of the distances covered during the fourth and third seconds is
View Solution
