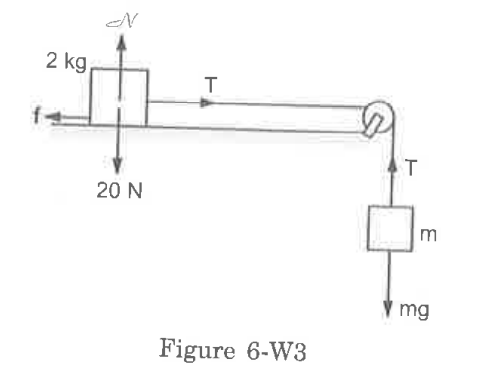
The coefficient of static friction between the block of 2 kg and the table shown in figure is μs=02. What should be the maximum value of m so that the blocks does not move? Take g=10m/s2. The string and the pulley are light and smooth.
0.4 kg
0.2 kg
0.1 kg
0.5 kg
The correct Answer is:A
Consider the equilibrium of the block of mass m. The forces on this block are
a. mg downward by the earth and
T upward by the string.
hence T−mg=0or,T=mg…….i
Now consider the equilibrium of the 2 kg block. The forces on this block are
a. T towards rightby the string,
b. f towards left (friction)by the table,
c. 20 N downward (weight) by the earth and
d. N upward (normal force) by the table
For vertical equilibrium of this block,
N=20N...........ii
A m is the largest mass which can be used without moving the system, the friction is limiting
Thus, f=μsN ...........iii
For horizontal equilibrium of the 2 kg block
f=T
Using equations i, iii and iv
μsN=mg
or 02×20N=mg
or, m=02×2010kg=04kg
Topper's Solved these Questions
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Short Answer
11 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Objective 1
10 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
Similar Questions
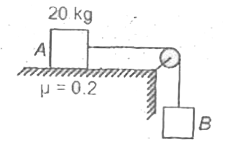
The coefficient of static friction, μs between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.(g=10m/s2)

View SolutionThe coefficient of static friction, μs between block A mass 2kg and the table as shown in the figure, is 0.2. What would be the maximum mass value of block B, so that the two blocks do not move ? The string and the pulley are asseumed to be smooth and massless (g=10m/s2)

View Solution
Knowledge Check
The coefficient of static friction between the block of 2 kg and the table shown in figure is μs=02. What should be the maximum value of m so that the blocks does not move? Take g=10m/s2. The string and the pulley are light and smooth.
 A0.4 kgB0.2 kgC0.1 kgD0.5 kg
A0.4 kgB0.2 kgC0.1 kgD0.5 kgThe coefficient of static friction μs between block A of mass 2kg and the table as shown in is 0.1 What would be the maximum mass value of blocks B so that the two bloks do not move ? The string and the pulley are assumed to be smooth and massless (g=10m/s2)
 .A0.2kgB0.4kgC2.0kgD4.0kg
.A0.2kgB0.4kgC2.0kgD4.0kgWhat should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10m/s2)
 A12 kgB8 kgC10 kgD6 kg
A12 kgB8 kgC10 kgD6 kg
A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=03, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
