figure shows two blocks connected by a light string placed on the two inclined parts of a triangular structure. The coefficients of static and inetic friction are 0.28 and 0.25 respectively at each of the surface. a.Find the minimum and maximum values of m for which the system remains at rest, b. Find the acceleration of either block if m is given the minimu value calculated in teh first part and is gentluy pushed up the incline for a short while.
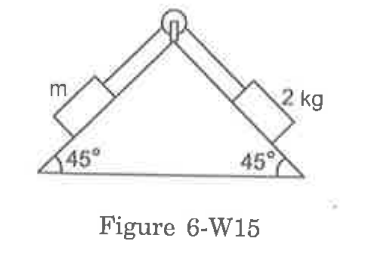
a. Take the 2 kg block as the system. The forces on this block are shown in ure with M=2 kg. It is assumed that m has its minimum value so that the 2 kg block has a tendency to slip down.As the block is in equilibrium, the resutant force shoud be zero.


Taking coponents ⊥ to the incline
N=Mgcos450=Mg√2.
Taking components || to the incline
T+f=Mgsin450=Mg√2. or T=Mg√2−f
As it is a case of limiting equilibrium.
f=μ2N
or T=Mg√2−μsMg√2=Mg√1−μ2............i
Now consider the other block as the system. the forces acting on this block are shown in ure.
Taking components ⊥ to the incline,
N'=mgcos450+f'=mg√2+f'
As it is the case of limiting equilirium
f'=μsN'=μsmg√2
Thus, T=mg√2(1+μs)
From i. and ii
m(1+μs)=M(1−μs)
or m=1−μs1+μsM=1−0.281+0.28×2kg
when maximum possible value of m is suplied the directions of friction are reversed becauyse m hs the tendency to sip down and 2 kg block to slip up. Thus, themaximum value of m can be obtained from iii by utting μ=−0.28.Thusthemaxiμmvalueofmisbrgt m=1+0.281−0.28×2kg<br>32/9kg<br>b.Ifm=9/8 kg andthesystemis≥ntlypushed,k∈eticictionwilloperate.Thus,<br>f=mu_k Mg/sqrt2 and f'(mu_kmg)/sqrt2
where μk=0.25. If the acceleration is a Newton's second law for M gives ure.
Mgsin450−T−f=Ma
or, Mg√2−T−μkMg√2Ma............iv
Applying Newton'ssecond law m ure.
T−mgsin450−f'=Ma
T−Mg√2−μkmkg√2=Maa...........v
Adding iv and v
Mg√2(1−μk)mg√2(1+μk)=(M+m)a
or, a=M(1−μk)−m(1+μk)√2(M+m)g
=2×0.75−98×1.25√2(2+98)g
=031ms2.
Topper's Solved these Questions
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Short Answer
11 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Objective 1
10 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
Similar Questions
Knowledge Check
Find the maximum value of (m//m) in the situation shown in figure so that the system remains at rest. Friction coefficient of both the contacts is μ , string is massless an pulley is friction less.
 Acosθsinθ−μcosθBsinθsinθ−μcosθCμcosθsinθ−μcosθDμsinθ−μcosθ
Acosθsinθ−μcosθBsinθsinθ−μcosθCμcosθsinθ−μcosθDμsinθ−μcosθTwo blocks A and B are connected by as string as shown in figure. Friction coefficient of the incline plane and block is 0.5. The mass of the block A is 5kg. If minimum & maximum values of masses of the block B for which the block remains in equilibrium are m1 & m2 then find value of (m2−m1).
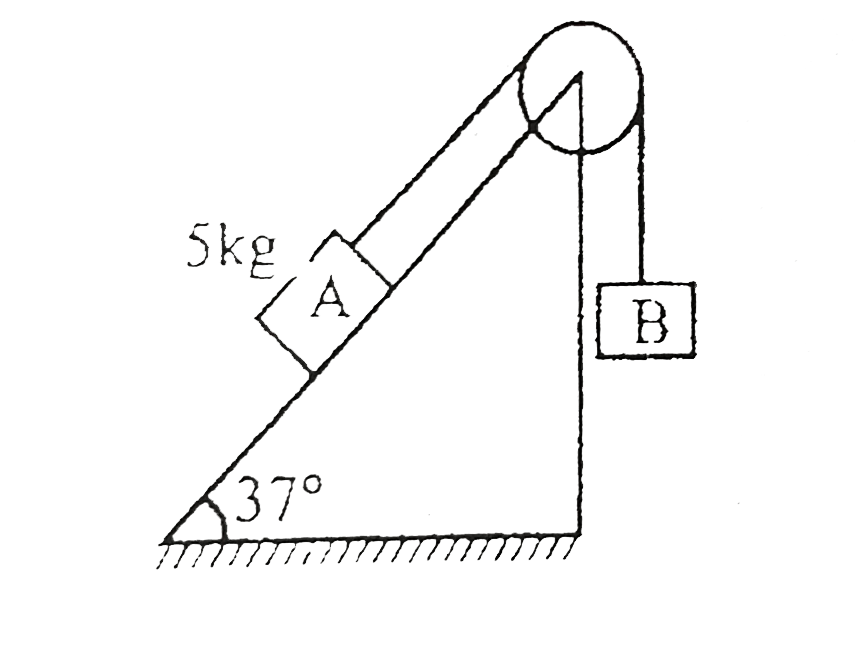 A4B6C3D2
A4B6C3D2A block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓
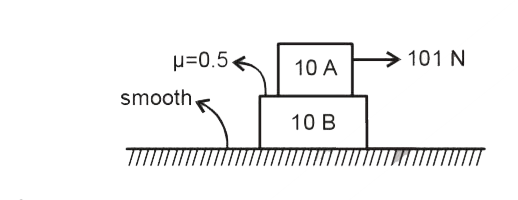
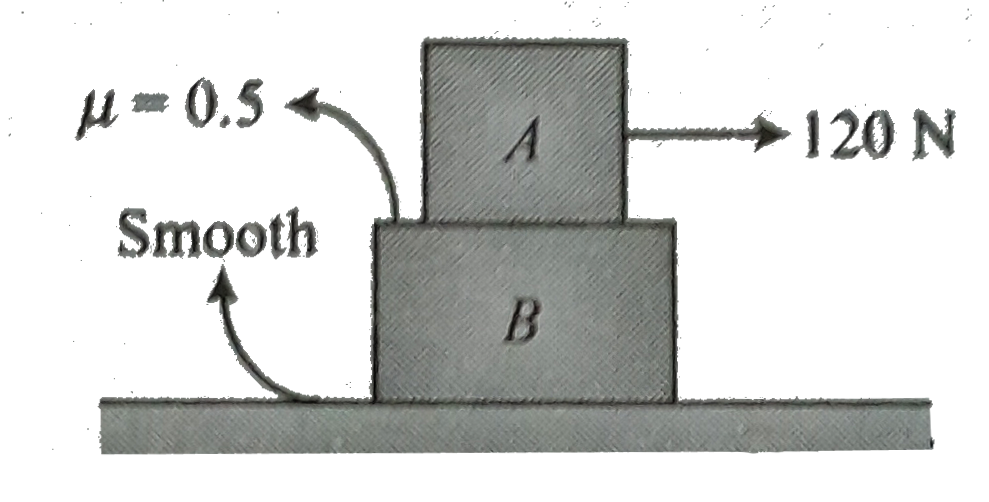
Find the acceleration of the two blocks . The system is initialy at rest and the friction are as shown in fig .Given mA=mB=10kg
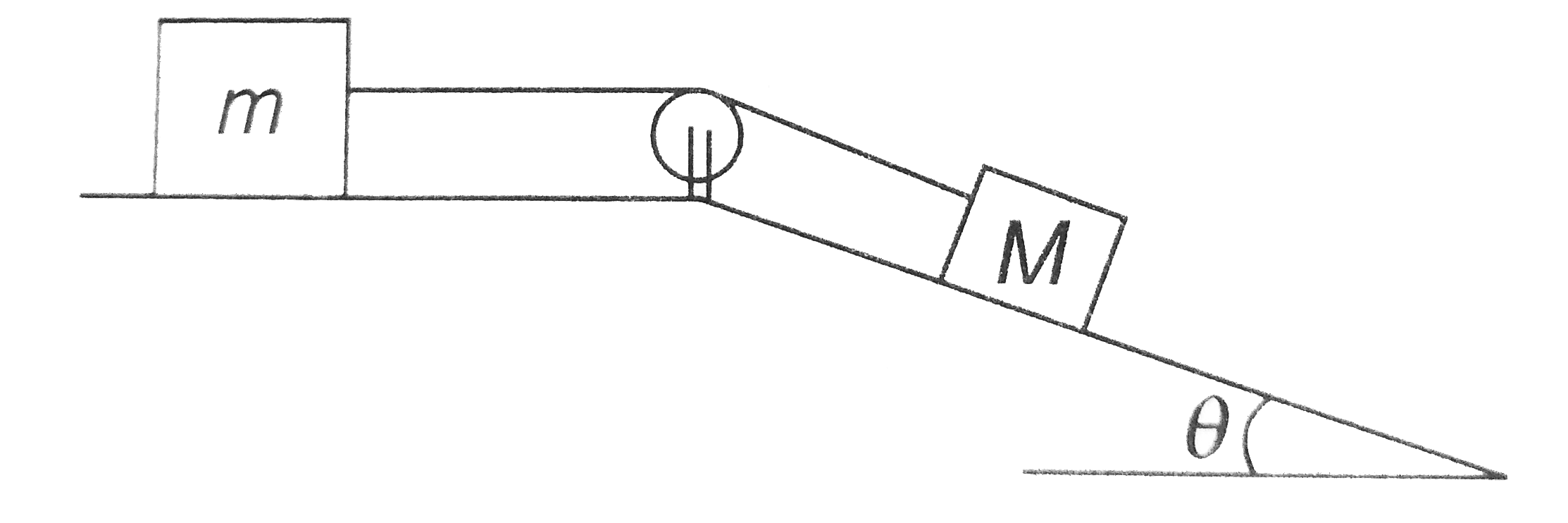
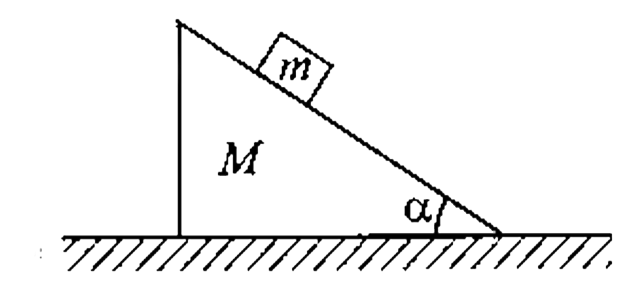
View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
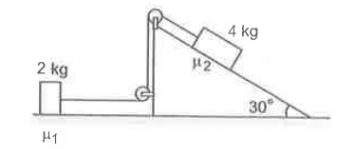
View SolutionIn the situation shown in fig
a. What minimum force F will make any part or whole system move?
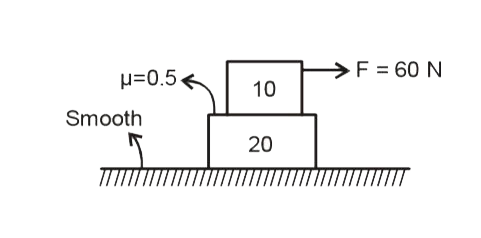
b. Find the acceleration of two blocks and value of friction at the two surface if F=6N
View SolutionIf the tension in the string in the figure. Is N and the acceleration of each block is 0.5ms2, find the friction coefficients at the two contacts with h blocks.
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.

View Solution