A car starts from rest on a half kilometer long bridge. The coefficiet of friction between the tyre and the road is 1.0. Show that one cannot drive thrugh the bridge in less than 10 s.
Let a maximum acceleratin is produced in car
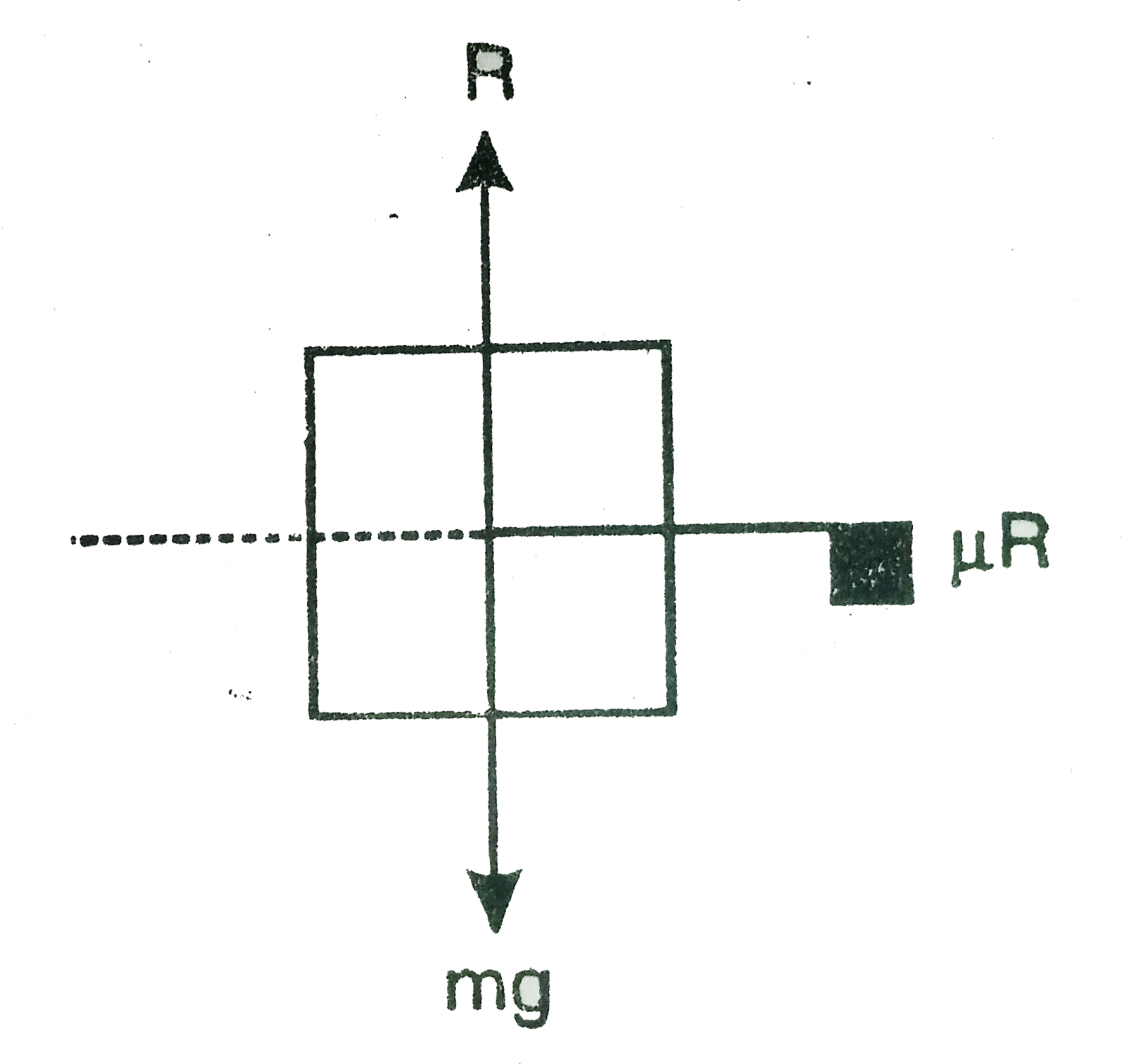
ma−μR
(for more accelerations the tyres will slip)
→ma=μmg
→a=μg=1×10=10ms2 Force crossing of the bridge in minimum time, it has to travel with maximum acceeleration.
u=0, S=500m, a=10m/s
FromS=ut+12at2
500=0+(12)10t2
→t=√100=10sec
If acceleration is less than 10ms2 timewill be more than 10 sec. So one can't drive throughthe bridge in less than 10 s.
Topper's Solved these Questions
Similar Questions
A car starts with a velocity of 100m/s on a half kilometre long bridge The coefficient of friction between the tyres and road is 0.1 Show that one cannot drive throught the bridge in less than 10s Take g=10m/s2.
View SolutionA car starts from rest on a 2−km long bridge. The coefficient of friction is 0.5. Find the minimum time to cross the bridge.
View Solution
Knowledge Check
A car starts from rest on a 1600m long bridge. The coefficient of friction between the tyre and road is 0.8. The minimum time taken by the car to cross the bridge is
A5sB10sC15sD20sA car starts from rest. It has to cover a distane of 500m from rest to rest. The coefficient of friction between the road and the tyre is 1/2. the minimum time in which the car can cover this distance is? (g=10m/s2)
A20sB10sC30sD15sA car moves at speed of 36 km hr−1on a level road. The coefficient of friction between the tyres and the road is 0.8 . The car negotiates a curve of radius R. IF g=10 ms−2, then the car will skid (or slip) while negotiating the curve if the value R is
A20 mB12 mC14 mD16 m
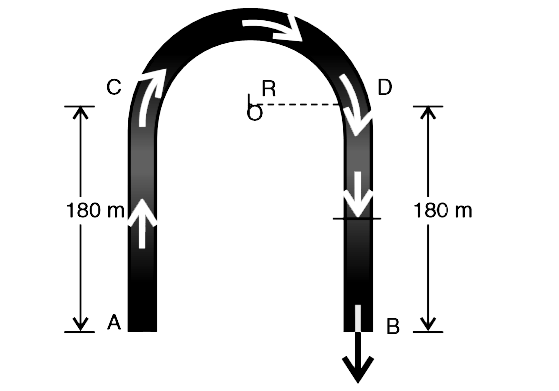
A flat race track consists of two straight section AC and DB each of length 180 m and one semi circular section DC of radius R = 150 m. A car starting from rest at A has to reach B in least possible time (the car may cross through point B and need not stop there). The coefficient of friction between the tyres and the road is μ=0.6 and the top speed that the car can acquire is 180 kph. Find the minimum time needed to move from A to B under ideal conditions. Braking is not allowed in the entire journey [g=10m/s2]
View SolutionA car starts from rest to cover a distance s. the coefficient of friction between the road and the tyres is μ. The minimum time in which the car can cover the distance is proportional to
View SolutionThe brakes of a car moving at 20 m/s along a horizontal road are suddenly applied and it comes to rest after travelling some distance if the coefficient of friction between the tyres and the road is 0.90 and it is assumed that all four tyres behave identically, the shortest distance the car would travel before coming to a stop is
View SolutionA van is moving with a speed of 108 km / hr on level road where the coefficient of fraction between the tyres and the road is 0.5 for the safe driving of the van , the minimum radius of curvature of the road will be ( g=10m/s2)
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the tyres and the road is 0.5, the shortest distance in which the car can be stopped is [g=10ms−1]
View Solution