A heavy mass m is hanging from a sting in equilibrium without breaking it. When this same mass is set into oscillation, the string breaks, Explain.
Step by step video & image solution for A heavy mass m is hanging from a sting in equilibrium without breaking it. When this same mass is set into oscillation, the string breaks, Explain. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 1
15 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective -1
1 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Worked Out Examples
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
A bob is released from the horizontal position of the inextensible string. If the breaking strength of the string is equal to twice the weight of the bob. Find the.
(A) Position where the string breaks.
(B) Time after which the bob strikes the ground measured from the instant of breaking of the sting.
(C ) Displacement of the bob from its point of breaking to the point of striking.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
The period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
A9:16B25:16C25:9D16:9A ball of mass 2kg hanging from a spring oscillates with a time period 2π seconds. Ball is removed when it is in equilibrium position, then spring shortens by
A10mB5mC20mD2πmA heavy particle of mass 0.50 kg is hanging from a string fixed with the roof. Find the force exerted by the string on the particle. Takeg=9.8ms2
 .AT is 9.9 N acting vertically upwardBT is 4.9 N acting vertically upwardCT is 4.9 N acting vertically downwardDT is 14.9 N acting vertically upward
.AT is 9.9 N acting vertically upwardBT is 4.9 N acting vertically upwardCT is 4.9 N acting vertically downwardDT is 14.9 N acting vertically upward
A heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length l connected to a celling. Determine the tension in the rope at a distance x from the ceiling.
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
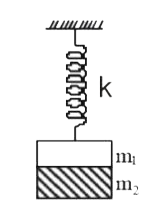
View SolutionA heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
View SolutionAn object of mass 0.75 kg is hanging from a string attached to roof.What will be the force applies by string on the object?
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View Solution
