What minimum horizontal speed should be given to the bob of a simple pendulum of length l so tht it describes a complete circle?

Video Solution

Text Solution

Verified by Experts

Suppose the bob is given a horizontal speed $v_{0}$ at the bottom and it describes a complete vetical circle. Let its speed at the highest point be v. Taking the gravitatioN/Al potenial energy to be zero at the bottom the conservastion of energy gives,
$\frac{1}{2} m \frac{v_{0}^{21}}{2} m v^{2} + 2 m g l$
or, $m v^{2} = m v_{0}^{2} - 4 m g l$ .......i

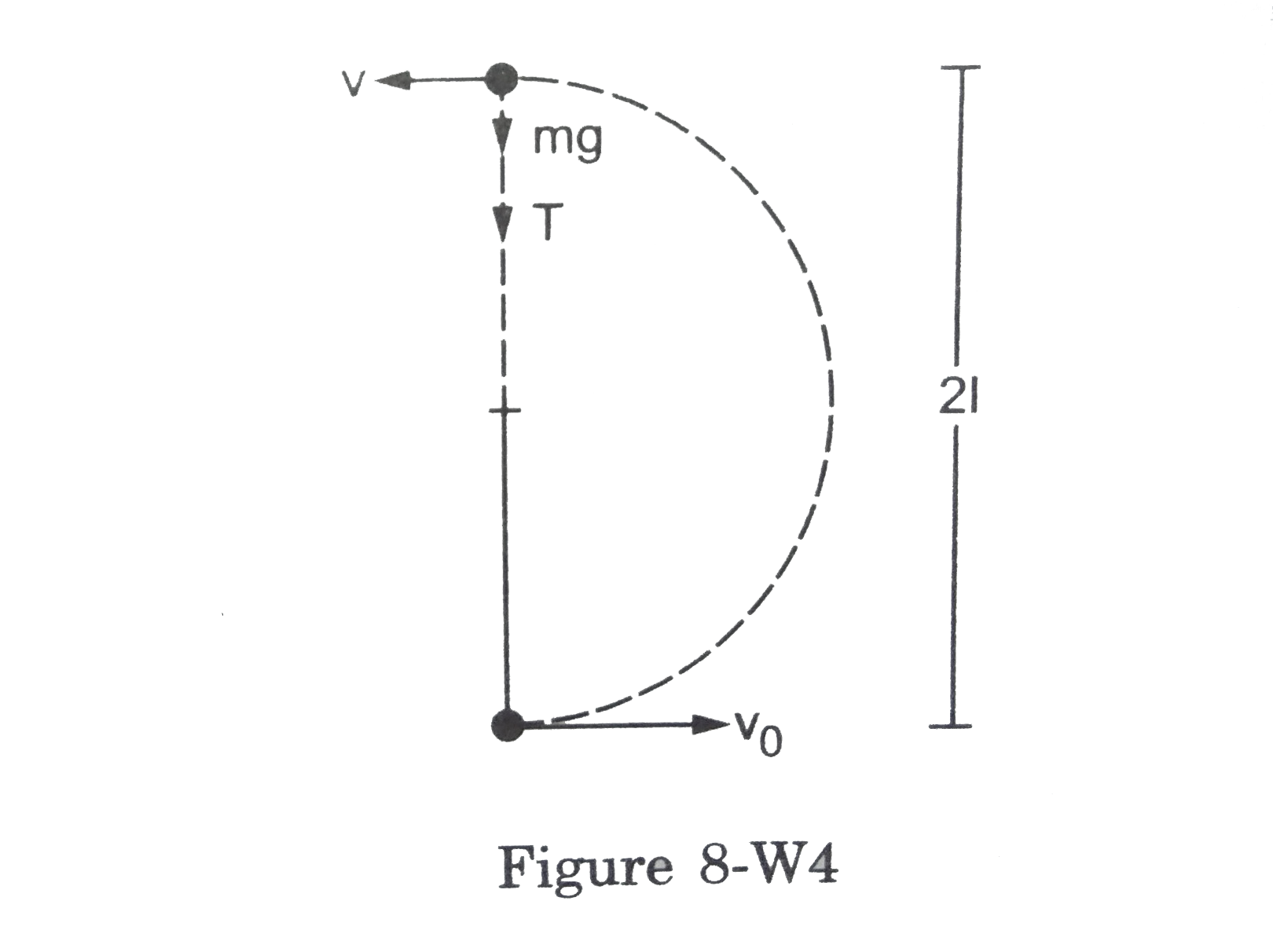
The forces acting on the bob at teh highest poit are mg due to the gravity and T due to the tension in teh string. The resultant force towards the cente is therefore, $m g + T$ . As the bob is moving in a circ,le, its acceleration towards the centre is $\frac{v^{2}}{l}$ . Applying Newton's second law and using i,
$m g + T = m \frac{v^{2}}{l} = \frac{1}{l} (m v_{0}^{2} - 4 m g l)$
or, $m v_{0}^{2} = 5 m g l + T l$
Now, for $v_{0}$ to be minimum T should be minimum. As the minimum value of T can be zero, for minimum speed,
$m v_{0}^{2} = 5 m g l or, v_{0} = \sqrt{5 g l}$

Updated on:21/07/2023

A body of mass m is suspended from a string of length l. What is minimum horizontal velocity that should be given to the body in its highest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle.
A $v = \sqrt{l g}$
B $v = \sqrt{2 l g}$
C $v = \sqrt{4 l g}$
D $v = \sqrt{5 l g}$
A body of mass m is suspended from a string of length l . What is minimum horizontal velocity that should be given to the body in its lowest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle
A $v = \sqrt{2 I g}$
B $v = \sqrt{3 I g}$
C $v = \sqrt{4 I g}$
D $v = \sqrt{5 I g}$
A simple pendulum of mass m and length l stands in equilibrium in vertical position .The maximum horizontal velocity that should be given to the bob at the bottom so that it completes on revolution is
A $\sqrt{l g}$
B $\sqrt{2 l g}$
C $\sqrt{3 l g}$
D $\sqrt{5 l g}$