Figure shows a loopthe loop track of raidus R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successful looping. Neglect friction.
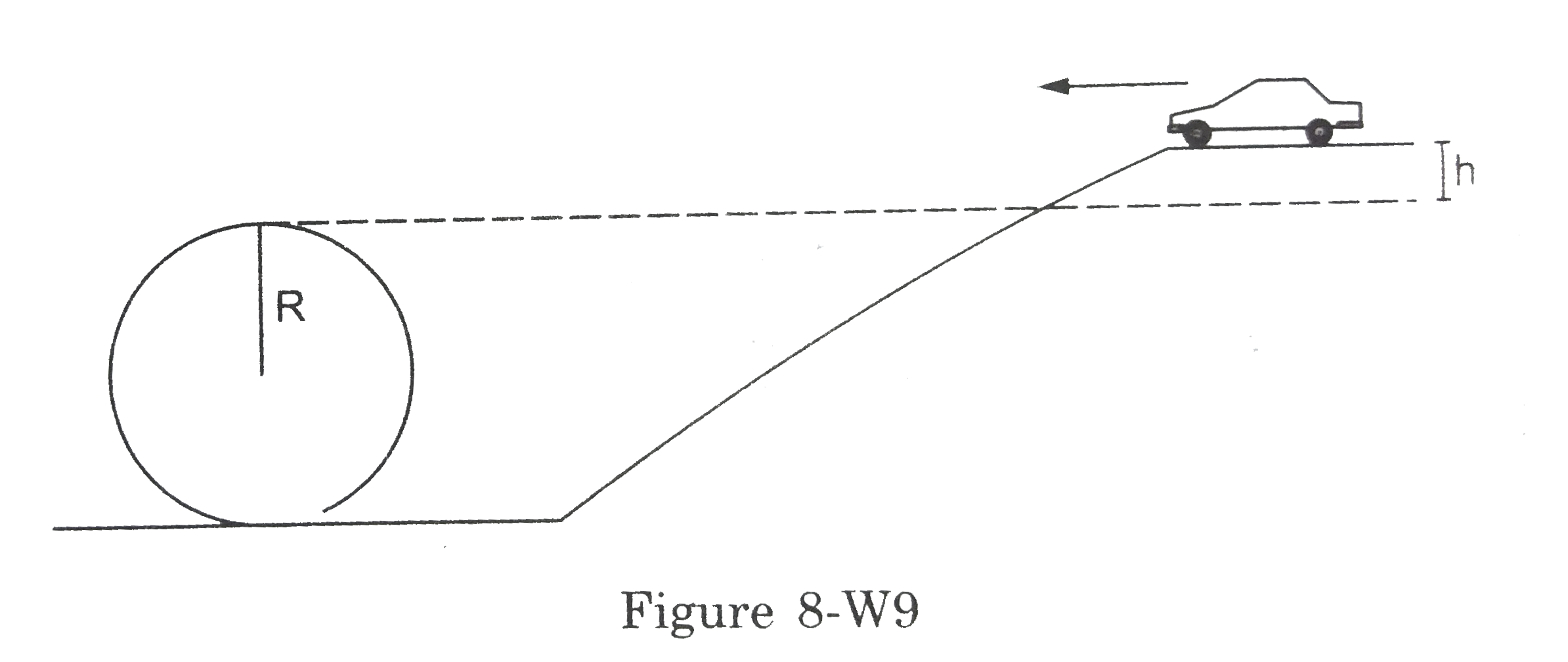
Suppose the speed of the car at the topmost point of the loop si v. Taking the gravitatioN/Al potential energy to be ero at the platform and assuming that the car starts with a negligible speed the conservation of energy shows
0=−mgh+12mv2
or, mv2=2mgh
where m is the mass of teh car. The car moving in a circle must have radial aceleration v2R at this instant. The force on the car are mg due to gravirty and N due to the contact with the tgrack. Both these forces are n radial direction at the top o the loop. Thus, from Newton's law
mg+N=mv2R
or, Mg+N=2mghR
For h to be minimum N should assume the minimum value which can be zero. Thus,
2mg(hmin)R=mgorhmin=R2
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Short Answer
15 Videos
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Objective 1
10 Videos
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises
64 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
Similar Questions
A small solid sphere rolls without slipping along the track shown in figure. The sphere starts from rest from a height h above the bottom of a loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is:

View SolutionA small toy car of mass m slides with negligible friction on a ''loop'' the loop track as shown in Fig.3E.32. The toy car starts from rest at a point H above the level of the lowest point of the track
(a) If H=2R, what normal force is exerted by the track on the toy car at point q?. What are the speed and normal force at point r ?
(b) At what height will the ball leave the track and to what maxiumum height will it rise afterwards ?
(c) If H=4R, what is the speed and normal reaction reaction at point s ?

View Solution
Knowledge Check
The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
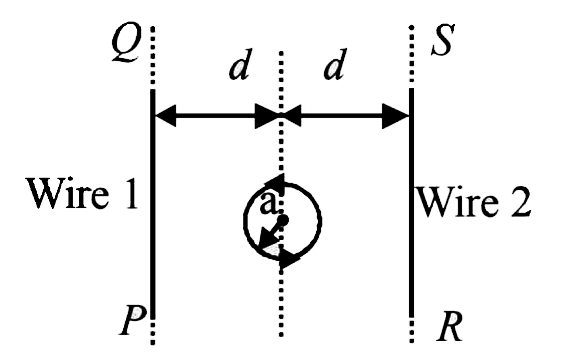
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseA(a) current in wire 1andwire2 in the direction PQandRS, respectively and h≈aB(b) current in wire 1andwire2 in the direction PQandSR, respectively and h≈aCcurrent in wire 1andwire2 in the direction PQandSR, respectively and h≈1.2aDcurrent in wire 1andwire2 in the direction PQandRS, respectively and h≈1.2aThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseAμ0I2a2dBμ0I2a22dC√3μ0I2a2dD√3μ0I2a22dA 1000 kg car starts from rest at point 1 and moves without friction down the track as shown in the figure. At point 2, the radius od curvature of the track is 6m.
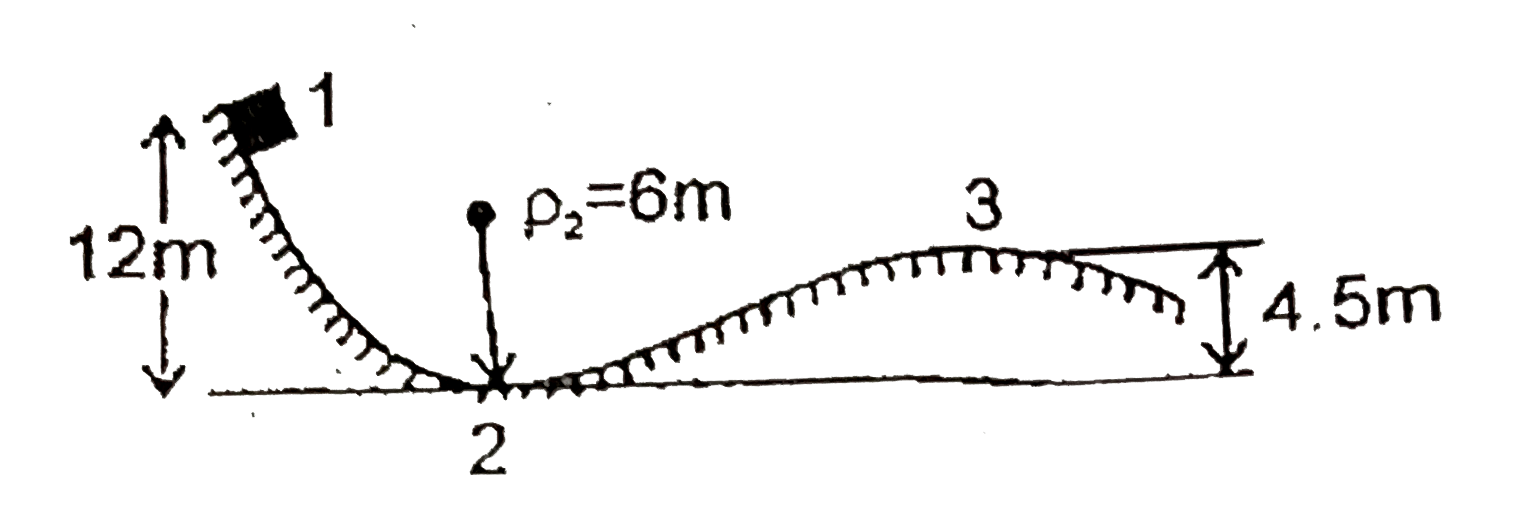 Athe force exerted by the track on the car at point 2 is 4000 kg wtBthe force exerted by the track on the car at point 2 is 5000 kg wtCthe minimum safe value of the radius of curvature at point 3 is 15 mDthe minium safe value of the radius of curvature at point 3 is 10 m
Athe force exerted by the track on the car at point 2 is 4000 kg wtBthe force exerted by the track on the car at point 2 is 5000 kg wtCthe minimum safe value of the radius of curvature at point 3 is 15 mDthe minium safe value of the radius of curvature at point 3 is 10 m
Figure shows a loop track whose lower part ends into a circular track of radius R and centre O.
A small solid sphere of mass M rolls without slipping along the loop track from the end A at a height 6R from the bottom of the track. What is the horizontal force acting on the sphere, when it rises up to the point P in level with the centre O of the circular part ?

View SolutionA frictionless tracke ABCDE ends in a circular loop of radius 'r' A body slides down the track from the point 'A' which is at a height h=10 cm . The maximum value of 'r' for the body to successful complete the loop is

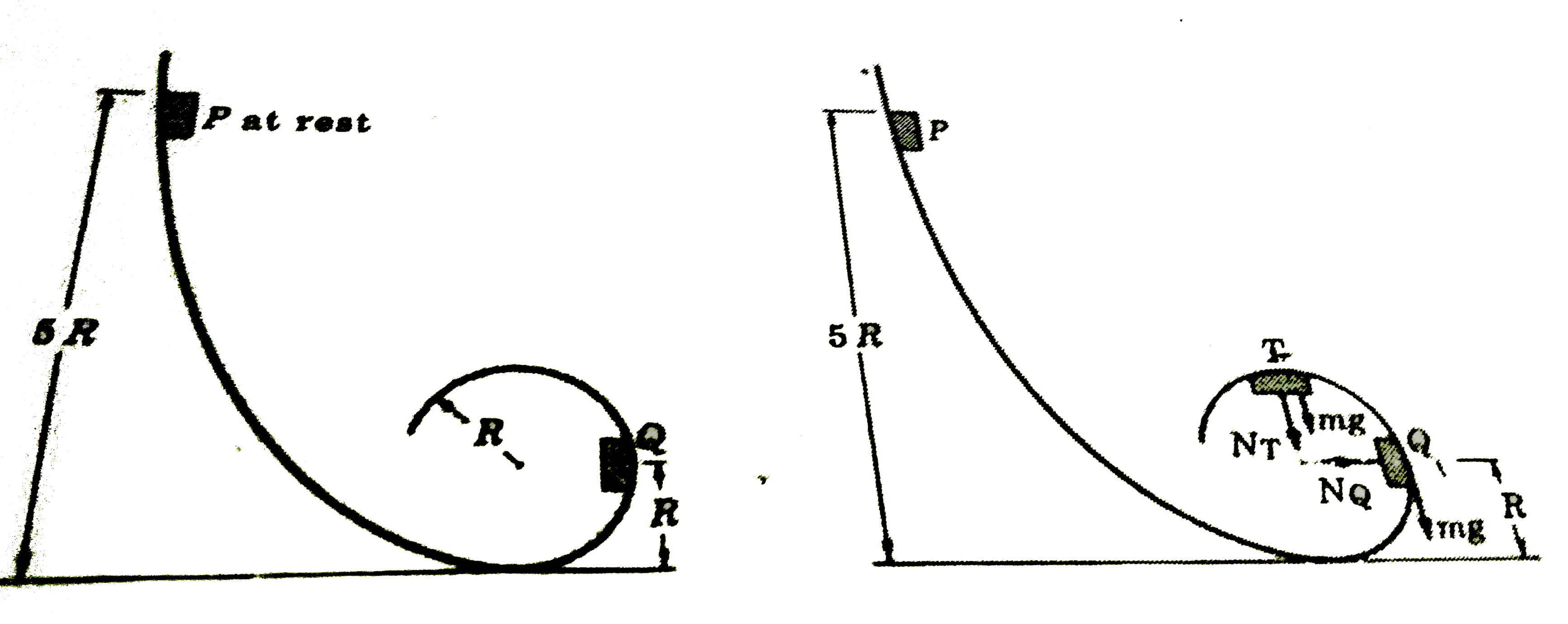
View SolutionA small block of mass m slides along a smooth track, as shown in fig. (i) If it starts from rest at P, what is the resulting force acting on it at Q ? (ii) at what height above the bottom of the loop should the block be released so that the force it exerts against the track at the top of the loop equals its weight?
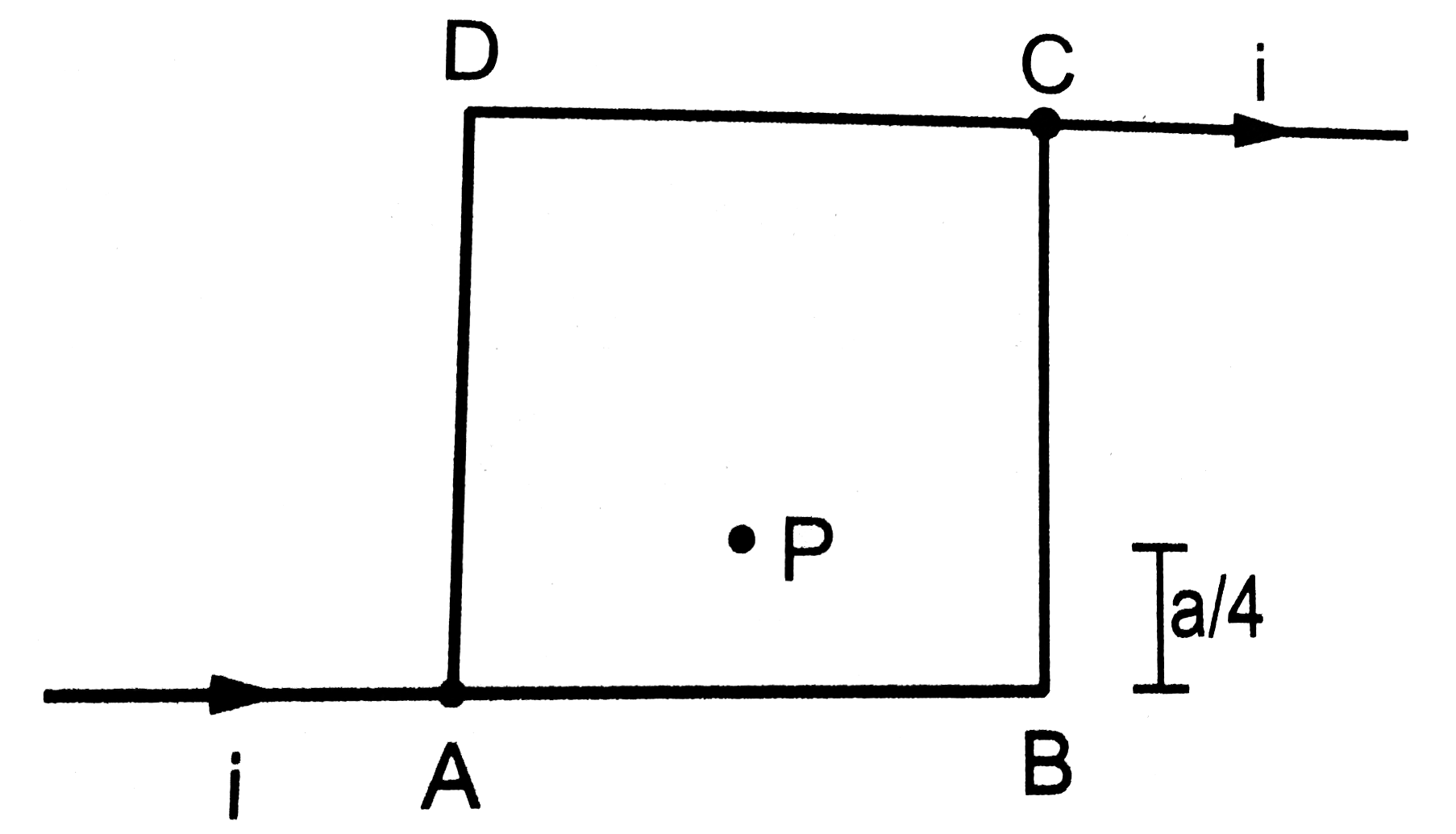
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View SolutionA small block of mass m slides along a smooth frictionless track as shown.
(a) If it starts from rest at P, what is the resultant force acting on it at Q?
(b) At what height above the bottom should the block be released so that the force it exerts against the track at the top of the loop equals its weight?

View Solution
