A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.

The torque applied to the wheel is
Γ=F.r=(20N)(0.20m)=4.0N−m.
the angular acceleration produced is
α=ΓI=4.0N−m0.20kg−m2=20rads2
The angular velocity after 5.0 seconds is
ω=ω0+αt=(20rads2)(5.0s)=100rads
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A wheel of moment of inertia 0.500kg−m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
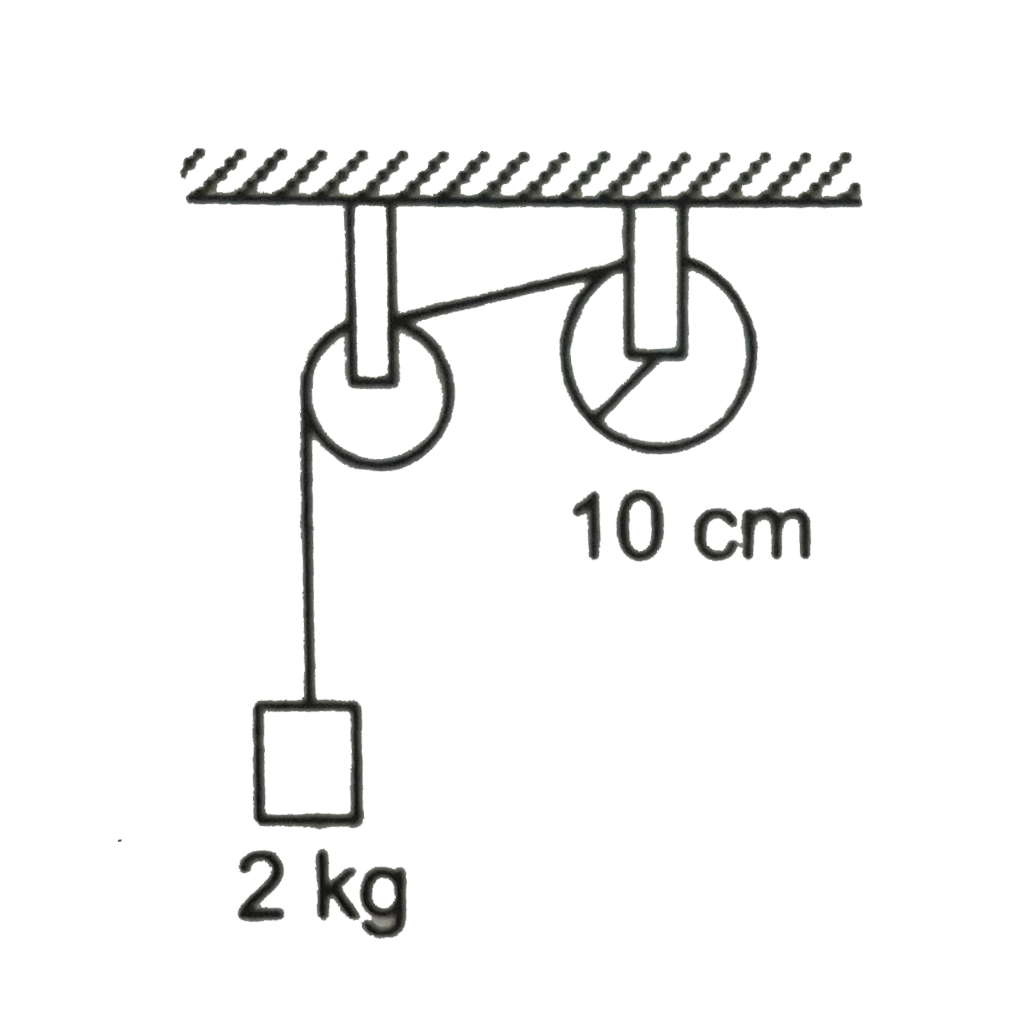
View Solution
Knowledge Check
A flywheel of moment of inertia 0.4 kg m2 and radius 0.2 m is free to rotate about a central axis. If a string is wrapped around it and it is pulled with a force of 10N. Then its angular velocity after 4s will be
A10rads−1B5rads−1C20rads−1DNoneA 50 N m torque acts on a wheel with a moment of inertia 150kg⋅m2. If the wheel starts from rest, how long will it take the wheel to make 1 rev?
A2.4 sB10 sC0.66 sD6.1 sA cord is wound round the circumference of a wheel of radius r. The axis of the wheel is horizontal and its moment of inertia about this axis is I. A weight mg is attached to the end of the cord and is allowed to fall from rest. The angular velocity of the wheel, when the weight has fallen through a distance h, is
A[2ghl+mr]1/2B[2mghI+mr2]1/2C[2mgh1+2mr2]1/2D(2gh)1/2
A pulley has the shape of a uniform solid disc of mass 2kg and radius 0.5m. A string is wrapped over its rim and is pulled by a force of 2.5N. The pulley is free to rotate about its axis. Initially, the pulley is at rest. Find the angular velocity and angle rotated by pulley in 10s.

View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
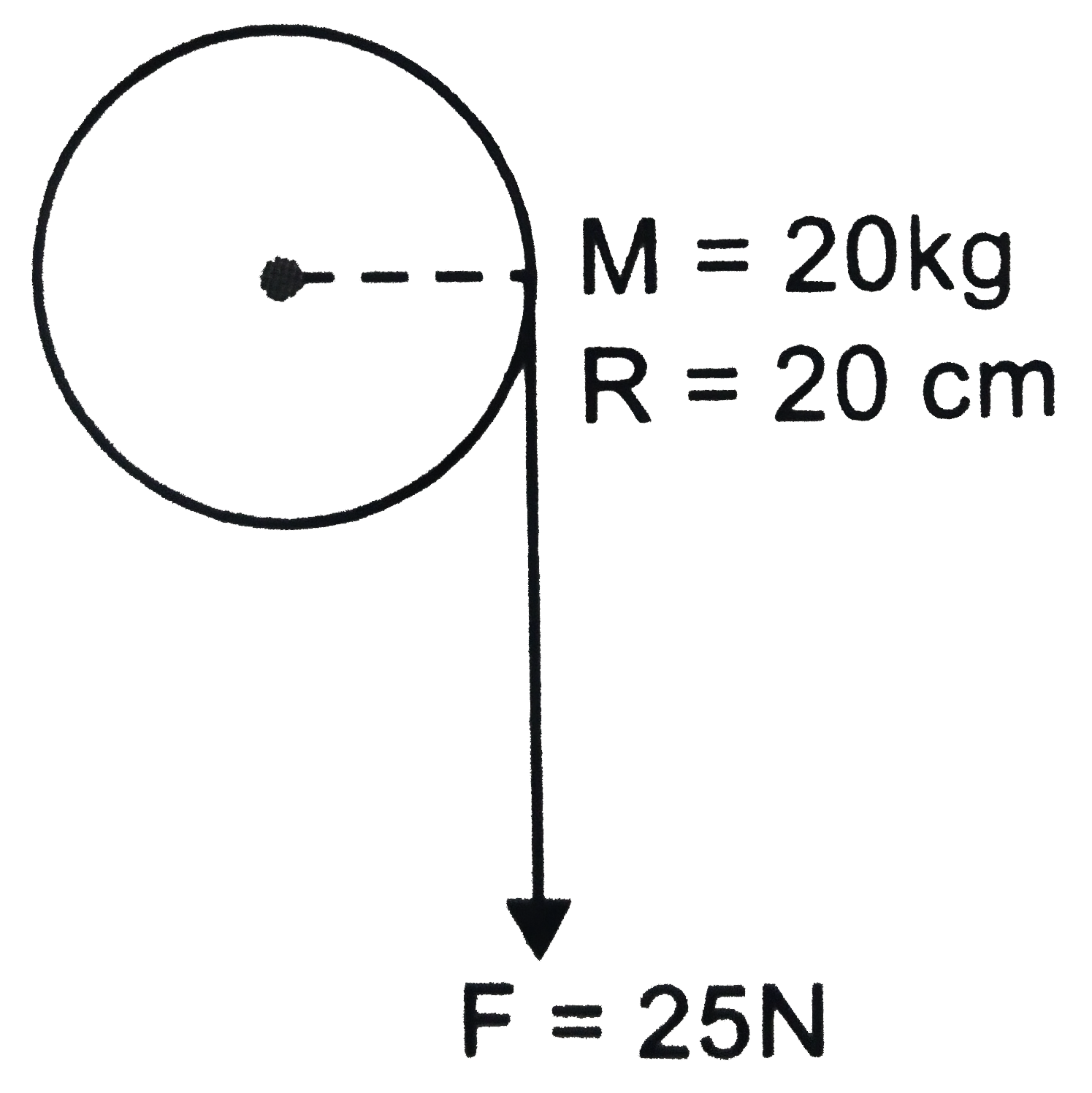
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
View SolutionA cord is wound around the circumference of wheel of radius r the axis of the wheel is horizontal and moment of inerita about it is / The weight mg is attached to the end of the cord and falls from rest after falling throgh a distance h the angular velocity of the wheel will be
View Solution
